题目内容
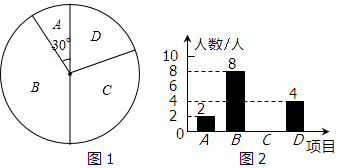
12.某学校为了增强学生体质,决定开放以下体育课外活动项目:A.篮球、B.乒乓球、C.跳绳、D.踢毽子.为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图(如图1,图2),请回答下列问题:(1)这次被调查的学生共有24人;
(2)请你将条形统计图补充完整.
分析 (1)用喜欢篮球的人数除以喜欢篮球的人数所占的百分比,即可求出这些被调查的学生数;
(2)用总人数减去喜欢篮球、乒乓球和踢毽子的人数,即可求出喜欢跳绳的人数,从而补全统计图.
解答 解:(1)根据题意得:2÷$\frac{30}{360}$=24(人),
则这次被调查的学生共有24人;
故答案为:24;
(2)喜欢跳绳的人数是:24-2-8-4=10(人),
补全图形,如图所示:
点评 本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.

练习册系列答案
相关题目
2.一个三角形三个内角的度数之比为1:4:5,这个三角形一定是( )
| A. | 等腰三角形 | B. | 直角三角形 | C. | 锐角三角形 | D. | 钝角三角形 |
7. 如图为二次函数y=ax2+bx+c的图象,A、B、C为抛物线与坐标轴的交点,且OA=OC=1,则下列关系中正确的是( )
如图为二次函数y=ax2+bx+c的图象,A、B、C为抛物线与坐标轴的交点,且OA=OC=1,则下列关系中正确的是( )
 如图为二次函数y=ax2+bx+c的图象,A、B、C为抛物线与坐标轴的交点,且OA=OC=1,则下列关系中正确的是( )
如图为二次函数y=ax2+bx+c的图象,A、B、C为抛物线与坐标轴的交点,且OA=OC=1,则下列关系中正确的是( )| A. | ac<0 | B. | b<2a | C. | a+b=-1 | D. | a-b=-1 |
17.如果x=2是关于x的方程x-3=a-x的解,则a的值是( )
| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
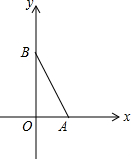 如图,在直角坐标系中,O为坐标原点,二次函数y=x2+mx+2的图象与x轴的正半轴交于点A,与y轴的正半轴交交于点B,且OA:OB=1:2.设此二次函数图象的顶点为D.
如图,在直角坐标系中,O为坐标原点,二次函数y=x2+mx+2的图象与x轴的正半轴交于点A,与y轴的正半轴交交于点B,且OA:OB=1:2.设此二次函数图象的顶点为D.