Question

18．如图，在平面直角坐标系中，O是坐标原点，点A的坐标为（-4，0），点B的坐标为（0，b）（b
＞0）．P是直线AB上的一个动点，作PC⊥x轴，垂足为C．记点P关于y轴的对称点为P′（点P′不在y轴上），连结PP′，P′A，P′C．设点P的横坐标为a．
（1）当b=3时，若点P′的坐标是（-1，m），求m的值；
（2）若点P在第一象限，记直线AB与P′C的交点为D，当P′D：P′C=1：4时，求a的值；
（3）s是否同时存在a、b，使△P′CA为等腰直角三角形？若存在，请求出所有满足要求的a，b的值；若不存在，请说明理由．

Answer 1

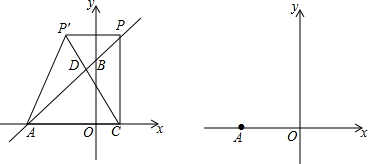
分析 （1）利用待定系数法先求出直线AB，再根据点P横坐标是-1代入直线AB解析式即可求解．
（2）根据平行线分线段成比例定理列出方程即可解决．
（3）分两种情形讨论即可：①如图2中，P′A=P′C，∠AP′C=90°，作P′H⊥AC，垂足为H，先证明四边形四边形PCHP′是正方形，然后列出方程解决．
②如图3中，∠CAP′=90°，AC=AP′，只要证明四边形PCAP′是正方形即可解决问题．

解答 解：（1）设直线AB为y=kx+b，由题意：$\left\{\begin{array}{l}{b=3}\\{-4k+b=0}\end{array}\right.$解得$\left\{\begin{array}{l}{k=\frac{3}{4}}\\{b=3}\end{array}\right.$，
所以直线AB为：y=$\frac{3}{4}$x+4，
当x=-1时．y=-$\frac{3}{4}$+4=$\frac{13}{4}$，所以m=$\frac{13}{4}$．
（2）如图1中，∵P′D：P′C=1：4，
∴P′D：DC=1：3，
∵PP′∥AC，
∴$\frac{PP′}{AC}=\frac{P′D}{DC}=\frac{1}{3}$，
∴$\frac{2a}{4+a}=\frac{1}{3}$，
∴a=$\frac{4}{5}$．
（3）存在，理由如下：
∵点P′不在y轴上，
∴∠P′CA≠90°
∴有两种情形：①如图2中，P′A=P′C，∠AP′C=90°，作P′H⊥AC，垂足为H，
∵P′H=P′C，P′H⊥AC，∠AP′C=90°
∴AH=HC=P′H，
∵P′H=CP，P′H∥PC，
∴四边形PCHP′是平行四边形，
∵P′H=HC，∠P′′HC=90°
∴四边形PCHP′是正方形，
∴PP′=HC，AC=2PP′，
∴4+a=4a，
∴a=$\frac{4}{3}$，PC=P′H=$\frac{1}{2}$AC=$\frac{8}{3}$，
∴点P（$\frac{4}{3}$，$\frac{8}{3}$），
∵OB∥PC，
∴$\frac{BO}{PC}=\frac{AO}{AC}$，
∴$\frac{BO}{\frac{8}{3}}=\frac{4}{\frac{16}{3}}$，
∴BO=2，
∴a=$\frac{4}{3}$，b=2．
②如图3中，∠CAP′=90°，AC=AP′，
∵PC∥P′A，PC=P′A，
∴四边形PCAP′是平行四边形，
∵P′A=AC，∠P′AC=90°
∴四边形PCAP′是正方形，
∴PP′=AC，AC=2PP′，
∴2a=4+a，
∴a=4，
∴AC=PC=8，
∵AO=OC=4，OB∥PC，
∴OB=$\frac{1}{2}$PC=4，
∴a=b=4．
综上所述：a=$\frac{4}{3}$，b=2或a=b=4时△ACP′是等腰直角三角形．

点评 本题考查了用待定系数法求一次函数的解析式、平行线分线段成比例定理、等腰三角形的性质，学会用分类讨论的思想是解决问题，正确画出图象是解决第三个问题的关键．