题目内容
13.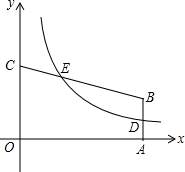 如图,四边形OABC放置在平面直角坐标系中,AB∥CO,OA所在直线为x轴,OC所在直线为y轴,反比例函数y=$\frac{k}{x}({k>0,x>0})$的图象经过AB的中点D,并且与CB交于点E,已知$\frac{CE}{CB}=\frac{1}{3},OC=\frac{7}{2}$.则AB的长等于( )
如图,四边形OABC放置在平面直角坐标系中,AB∥CO,OA所在直线为x轴,OC所在直线为y轴,反比例函数y=$\frac{k}{x}({k>0,x>0})$的图象经过AB的中点D,并且与CB交于点E,已知$\frac{CE}{CB}=\frac{1}{3},OC=\frac{7}{2}$.则AB的长等于( )| A. | 2.5 | B. | 2 | C. | 1.5 | D. | 1 |
分析 根据题意结合相似三角形的判定与性质得出$\frac{NV}{NB}$=$\frac{EC}{CB}$,进而表示出E,D点坐标,再利用反比例函数图象点的性质得出答案.
解答 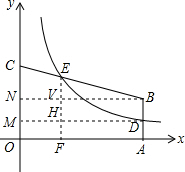 解:如图所示:过点E作EF⊥OA于点F,BN⊥CO于点N,DM⊥CO于点M,
解:如图所示:过点E作EF⊥OA于点F,BN⊥CO于点N,DM⊥CO于点M,
∵反比例函数y=$\frac{k}{x}({k>0,x>0})$的图象经过AB的中点D,
∴设AD=a,AO=3b,则AB=2a,
可得EF∥CO,
则△BEV∽△BCN,
∵$\frac{EC}{CB}$=$\frac{1}{3}$,CO=$\frac{7}{2}$,
∴$\frac{NV}{NB}$=$\frac{EC}{CB}$=$\frac{1}{3}$,
∴NV=b,
由题意可得:CN=$\frac{7}{2}$-2a,
$\frac{EV}{CN}$=$\frac{BE}{BC}$=$\frac{2}{3}$,
则$\frac{EV}{\frac{7}{2}-2a}$=$\frac{2}{3}$,
解得:EV=$\frac{7}{3}$-$\frac{4}{3}$a,
故EF=$\frac{7}{3}$-$\frac{4}{3}$a+2a=$\frac{7}{3}$+$\frac{2}{3}$a,
∴E(b,$\frac{7}{3}$+$\frac{2}{3}$a),D(3b,a),
故b($\frac{7}{3}$+$\frac{2}{3}$a)=3ab,
解得:a=1,
则AB=2a=2.
故选:B.
点评 此题主要考查了相似三角形的判定与性质以及反比例函数图象上点的坐标性质,正确表示出D,E点坐标是解题关键.

练习册系列答案
相关题目
1.方程3x(x-1)=2(x-1)的解是( )
| A. | x=1 | B. | x=$\frac{2}{3}$ | C. | x1=1,x2=$\frac{2}{3}$ | D. | x1=1,x2=-$\frac{2}{3}$ |
8.下列计算不正确的是( )
| A. | (-3)0=-1 | B. | 3.8×10-5=0.000038 | ||
| C. | 20020=20030 | D. | ($\frac{1}{4}$)-2=16 |
5.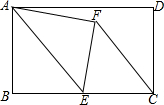 如图,在矩形ABCD中,AB=8,BC=12,点E是BC的中点,连接AE,将△ABE沿AE折叠,点B落在点F处,连接FC,则tan∠ECF=( )
如图,在矩形ABCD中,AB=8,BC=12,点E是BC的中点,连接AE,将△ABE沿AE折叠,点B落在点F处,连接FC,则tan∠ECF=( )
 如图,在矩形ABCD中,AB=8,BC=12,点E是BC的中点,连接AE,将△ABE沿AE折叠,点B落在点F处,连接FC,则tan∠ECF=( )
如图,在矩形ABCD中,AB=8,BC=12,点E是BC的中点,连接AE,将△ABE沿AE折叠,点B落在点F处,连接FC,则tan∠ECF=( )| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
2.方程x+2=3的解是( )
| A. | 3 | B. | -3 | C. | 1 | D. | -1 |
 如图,在平面直角坐标系中,△CDE的顶点C点坐标为C(1,-2),点D的横坐标为$\frac{19}{5}$,将△CDE绕点C旋转到△CBO,点D的对应点B在x轴上.抛物线y=ax2+bx+c以点C为顶点,且经过点B,它与x轴的另一个交点为点A.
如图,在平面直角坐标系中,△CDE的顶点C点坐标为C(1,-2),点D的横坐标为$\frac{19}{5}$,将△CDE绕点C旋转到△CBO,点D的对应点B在x轴上.抛物线y=ax2+bx+c以点C为顶点,且经过点B,它与x轴的另一个交点为点A. 如图,正方形ABCD中,点O是对角线AC、BD的交点,点E在CD上,且DE=2CE,连接BE,过点C作CF⊥BE于F,连接OF,已知EF=1,则OF的长为3$\sqrt{2}$.
如图,正方形ABCD中,点O是对角线AC、BD的交点,点E在CD上,且DE=2CE,连接BE,过点C作CF⊥BE于F,连接OF,已知EF=1,则OF的长为3$\sqrt{2}$. 如图,在平面直角坐标系中,抛物线y=ax2+bx+c的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点A、C的坐标分别为(-1,0),(0,-3),直线x=1为抛物线的对称轴,点D为抛物线的顶点,直线BC与对称轴相交于点E.
如图,在平面直角坐标系中,抛物线y=ax2+bx+c的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点A、C的坐标分别为(-1,0),(0,-3),直线x=1为抛物线的对称轴,点D为抛物线的顶点,直线BC与对称轴相交于点E.