题目内容
20.在?ABCD中,∠ABC的平分线交直线AD于点E,且AE=5,ED=2,则?ABCD的周长是24或16.分析 由平行四边形ABCD得到AB=CD,AD=BC,AD∥BC,再和已知BE平分∠ABC,进一步推出∠ABE=∠AEB,即AB=AE,即可求出AB、AD的长,就能求出答案.
解答  解:如图1:∵四边形ABCD是平行四边形,
解:如图1:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,AD∥BC,
∴∠AEB=∠EBC,
∵BE平分∠ABC,
∴∠ABE=∠EBC,
∴∠ABE=∠AEB,
∵AE=5,
∴AB=AE=5,
∴AD=AE+DE=5+2=7,
∴AB=CD=5,AD=BC=7,
∴平行四边形的周长是2(AB+BC)=24;
如图2:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,AD∥BC,
∴∠AEB=∠EBC,
∵BE平分∠ABC,
∴∠ABE=∠EBC,
∴∠ABE=∠AEB,
∵AE=5,
∴AB=AE=5,
∴AD=AE-DE=5-2=3,
∴AB=CD=5,AD=BC=3,
∴平行四边形的周长是2(AB+BC)=16.
故答案为:24或16.
点评 本题主要考查了平行四边形的性质,在平行四边形中,当出现角平分线时,一般可构造等腰三角形,进而利用等腰三角形的性质解题.

练习册系列答案
相关题目
15.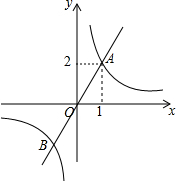 如图,函数y1=$\frac{k_1}{x}$与y2=k2x的图象相交于点A(1,2)和点B,当y1<y2时,自变量x的取值范围是( )
如图,函数y1=$\frac{k_1}{x}$与y2=k2x的图象相交于点A(1,2)和点B,当y1<y2时,自变量x的取值范围是( )
 如图,函数y1=$\frac{k_1}{x}$与y2=k2x的图象相交于点A(1,2)和点B,当y1<y2时,自变量x的取值范围是( )
如图,函数y1=$\frac{k_1}{x}$与y2=k2x的图象相交于点A(1,2)和点B,当y1<y2时,自变量x的取值范围是( )| A. | -1<x<0或x>1 | B. | x<-1或0<x<1 | C. | x>1 | D. | -1<x<0 |
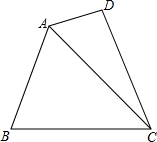 如图,在四边形ABCD中,AC平分∠BAD,且AC=BC,AB=2AD.
如图,在四边形ABCD中,AC平分∠BAD,且AC=BC,AB=2AD.
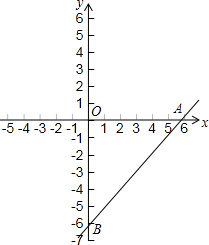 直线y=x-6与x轴、y轴分别交于A、B两点,点E从B点出发,以每秒1个单位长度的速度沿线段BO向O点移动(不考虑点E与B、O两点重合的情况),过点E作EF∥AB,交x轴于点F,将四边形ABEF沿直线EF折叠后,与点A对应的点记作点C,与点B对应的点记作点D,得到四边形CDEF,设点E的运动时间为t秒.
直线y=x-6与x轴、y轴分别交于A、B两点,点E从B点出发,以每秒1个单位长度的速度沿线段BO向O点移动(不考虑点E与B、O两点重合的情况),过点E作EF∥AB,交x轴于点F,将四边形ABEF沿直线EF折叠后,与点A对应的点记作点C,与点B对应的点记作点D,得到四边形CDEF,设点E的运动时间为t秒.