题目内容
10.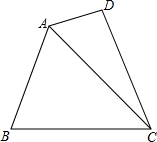 如图,在四边形ABCD中,AC平分∠BAD,且AC=BC,AB=2AD.
如图,在四边形ABCD中,AC平分∠BAD,且AC=BC,AB=2AD.(1)求∠ADC的度数;
(2)若AB=10cm,CD=12cm,求四边形ABCD的面积.
分析 (1)作CE⊥AB交AB于点E,则∠AEC=90°,利用已知条件和全等三角形的判定方法可证明△ADC≌△AEC,利用全等三角形的性质即可得到∠ADC=∠AEC=90°;
(2)由(1)可知S△ACD=S△AEC,再根据高相等的两个三角形面积比等于底之比可得S△ACB=2S△ADC,进而四边形ABCD的面积=3S△ADC,问题得解.
解答 解:(1)作CE⊥AB交AB于点E,则∠AEC=90°,
∵AC=BC,
∴CE是AB的垂直平分线,
∴AE=BE=$\frac{1}{2}$AB,
∵AB=2AD,
∴AE=AD=$\frac{1}{2}$AB,
∵∠AC平分∠BAD,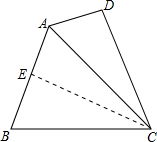
∴∠EAC=∠DAC,
在△ADC和△AEC中,
$\left\{\begin{array}{l}{AD=AE}\\{∠EAC=∠DAC}\\{AC=AC}\end{array}\right.$,
∴△ADC≌△AEC,
∴∠ADC=∠AEC=90°;
(2)∵CE是AB的垂直平分线,
∴S△ACD=S△AEC,
∵AB=2AD,CD=CE,
∴S△ACB=2S△ADC,
∴四边形ABCD的面积=3S△ADC=3×$\frac{1}{2}$×5×12=90cm2.
点评 本题考查了全等三角形的判定和性质以及求不规则四边形的面积,解题的关键是正确添加辅助线构造全等三角形,题目的综合性较强,难度中等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.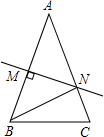 如图,在三角形ABC中,AB=AC,∠A=36°,AB的垂直平分线MN交AB于点M,交AC于点N,下面结论:①BN平分∠ABC;②△BCN是等腰三角形;③△BMN≌△BCN;④△BCN的周长等于AB+BC,其中正确的结论是( )
如图,在三角形ABC中,AB=AC,∠A=36°,AB的垂直平分线MN交AB于点M,交AC于点N,下面结论:①BN平分∠ABC;②△BCN是等腰三角形;③△BMN≌△BCN;④△BCN的周长等于AB+BC,其中正确的结论是( )
 如图,在三角形ABC中,AB=AC,∠A=36°,AB的垂直平分线MN交AB于点M,交AC于点N,下面结论:①BN平分∠ABC;②△BCN是等腰三角形;③△BMN≌△BCN;④△BCN的周长等于AB+BC,其中正确的结论是( )
如图,在三角形ABC中,AB=AC,∠A=36°,AB的垂直平分线MN交AB于点M,交AC于点N,下面结论:①BN平分∠ABC;②△BCN是等腰三角形;③△BMN≌△BCN;④△BCN的周长等于AB+BC,其中正确的结论是( )| A. | ①②③ | B. | ①②④ | C. | ②③④ | D. | ①③④ |
2.下列各数中,是无理数的是( )
| A. | $\frac{22}{7}$ | B. | 0.101001 | C. | $\sqrt{81}$ | D. | $\sqrt{32}$ |
 已知:如图∥AD,∠1=∠2,∠BAC=60°,求∠AGD的度数.
已知:如图∥AD,∠1=∠2,∠BAC=60°,求∠AGD的度数.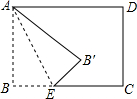 如图,将长方形ABCD沿直线AE折叠,点B落在点B′处,已知BC=8,AB=6,若△B′EC为直角三角形,则BE的长为3或6或$\frac{25}{3}$.
如图,将长方形ABCD沿直线AE折叠,点B落在点B′处,已知BC=8,AB=6,若△B′EC为直角三角形,则BE的长为3或6或$\frac{25}{3}$.
 已知:线段a,b.求作:△ABC,使AB=AC=b,且BC边上的高AD=a(不写作法,只保留作图痕迹)
已知:线段a,b.求作:△ABC,使AB=AC=b,且BC边上的高AD=a(不写作法,只保留作图痕迹)