题目内容
解分式方程: 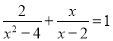
 .
【解析】试题分析:首先进行去分母,将分式方程转化为整式方程,然后求出方程的解,最后需要对方程的解进行检验,看是否能使原分式的分母为零.
试题解析:去分母得:2+x(x+2)=x2-4, 解得:x=-3,
检验:当x=-3时,(x+2)(x-2)≠0,
故x=-3是原方程的根.
.
【解析】试题分析:首先进行去分母,将分式方程转化为整式方程,然后求出方程的解,最后需要对方程的解进行检验,看是否能使原分式的分母为零.
试题解析:去分母得:2+x(x+2)=x2-4, 解得:x=-3,
检验:当x=-3时,(x+2)(x-2)≠0,
故x=-3是原方程的根.
练习册系列答案
相关题目
若对于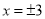 以外的一切数
以外的一切数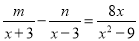 均成立,则
均成立,则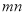 的值是( )
的值是( )
A. 8 B. 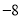 C. 16 D.
C. 16 D. 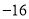
 D
【解析】,则 ,得: .
故选D.
D
【解析】,则 ,得: .
故选D. 使分式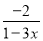 的值为正的条件是( )
的值为正的条件是( )
A. 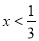 B.
B. 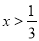 C. x<0 D. x>0
C. x<0 D. x>0
 B
【解析】由题意得
1-3x<0,
解之得
.
故选B.
B
【解析】由题意得
1-3x<0,
解之得
.
故选B. 如图所示,在?ABCD中,对角线AC,BD相交于点O,E,F是对角线AC上的两点,当E,F满足下列哪个条件时,四边形DEBF不一定是平行四边形( )
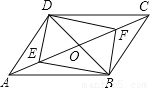
A.OE=OF B.DE=BF C.∠ADE=∠CBF D.∠ABE=∠CDF
 B.
【解析】
试题分析:A、∵四边形ABCD是平行四边形,∴OD=OB,又∵OE=OF,∴四边形DEBF是平行四边形.能判定是平行四边形.B、DE=BF,OD=OB,缺少夹角相等.不能利用全等判断出OE=OF,∴DE=BF,∴四边形DEBF不一定是平行四边形.C、D均能证明四边形DEBF是平行四边形.
故选:B.
B.
【解析】
试题分析:A、∵四边形ABCD是平行四边形,∴OD=OB,又∵OE=OF,∴四边形DEBF是平行四边形.能判定是平行四边形.B、DE=BF,OD=OB,缺少夹角相等.不能利用全等判断出OE=OF,∴DE=BF,∴四边形DEBF不一定是平行四边形.C、D均能证明四边形DEBF是平行四边形.
故选:B. 一个多边形的内角和与外角和的度数之比为2∶1,则这个多边形的边数为( )
A. 3 B. 4 C. 5 D. 6
 D
【解析】设这个多边形有n条边,由题意得
(n-2) ×180:360=2:1,
解之得
n=6.
故选D.
D
【解析】设这个多边形有n条边,由题意得
(n-2) ×180:360=2:1,
解之得
n=6.
故选D. 分式方程 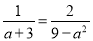 的解是_______.
的解是_______.
 1
【解析】去分母得:3-a=2,解得:a=1,检验:当a=1时,9-a²≠0,所以原方程的解是:a=1.故答案为:a=1.
1
【解析】去分母得:3-a=2,解得:a=1,检验:当a=1时,9-a²≠0,所以原方程的解是:a=1.故答案为:a=1. 分式方程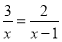 的解是( )
的解是( )
A. 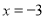 B.
B. 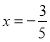 C.
C. 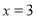 D. 无解
D. 无解
 C.
【解析】
试题分析:分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
去分母得:3x-3=2x,
解得:x=3,
经检验x=3是分式方程的解.
故选C.
考点: 解分式方程.
C.
【解析】
试题分析:分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
去分母得:3x-3=2x,
解得:x=3,
经检验x=3是分式方程的解.
故选C.
考点: 解分式方程. (2016内蒙古包头市)化简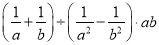 ,其结果是( )
,其结果是( )
A. 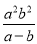 B.
B. 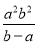 C.
C. 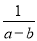 D.
D. 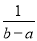
 B
【解析】= .
所以选B.
B
【解析】= .
所以选B. 等腰△ABC中,AB=AC,一边上的中线BD将这个三角形的周长分为15和12两个部分,则这个等腰三角形的底边长为( )
A. 7 B. 11 C. 7或11 D. 7或10
 C
【解析】试题分析:题中给出了周长关系,要求底边长,首先应先想到等腰三角形的两腰相等,寻找问题中的等量关系,列方程求解,然后结合三角形三边关系验证答案.设等腰三角形的底边长为x,腰长为y,则根据题意,得①或②,解方程组①得:x=11,y=8,根据三角形三边关系定理,此时能组成三角形;解方程组②得:x=7,y=10,根据三角形三边关系定理此时能组成三角形,即等腰三角形的底边长是11或7.
...
C
【解析】试题分析:题中给出了周长关系,要求底边长,首先应先想到等腰三角形的两腰相等,寻找问题中的等量关系,列方程求解,然后结合三角形三边关系验证答案.设等腰三角形的底边长为x,腰长为y,则根据题意,得①或②,解方程组①得:x=11,y=8,根据三角形三边关系定理,此时能组成三角形;解方程组②得:x=7,y=10,根据三角形三边关系定理此时能组成三角形,即等腰三角形的底边长是11或7.
... 
