题目内容
10.我们约定,在平面直角坐标系xOy中,经过象限内某点且平行于坐标轴或平行于两坐标轴夹角平分线的直线,叫该点的“参照线”.例如,点M(1,3)的参照线有:x=1,y=3,y=x+2,y=-x+4(如图1).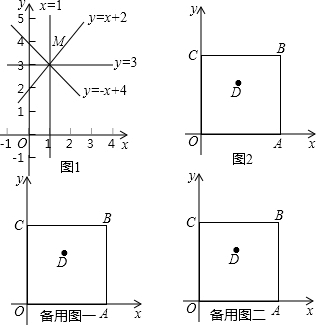
如图2,正方形OABC在平面直角坐标系xOy中,点B在第一象限,点A,C分别在x轴和y轴上,点D(m,n)在正方形内部.
(1)直接写出点D的所有参照线:x=m,y=n,y=x+n-m,y=-x+n+m;
(2)若A(6,0),点D在线段OA的垂直平分线上,且点D有一条参照线是y=-x+7,则点D的坐标是(3,4);
(3)在(2)的条件下,点P是AB边上任意一点(点P不与点A,B重合),连接OP,将△OAP沿着OP折叠,点A的对应点记为A′,当点A′在点D的平行于坐标轴的参照线上时,写出相应的点P的坐标(6,2$\sqrt{3}$)或(6,9-3$\sqrt{5}$).
分析 (1)根据参照线的定义可知,点D(m,n)的所有参照线为:x=m,y=n,y=x+n-m,y=-x+n+m;
(2)利用待定系数法即可解决问题;
(3)分两种情形①如图1中,当点A′在参照线HM上时,设PA=PA′=x.②如图2中,当点A′在参照线DH上时,设PA=PA′=y.分别构建方程即可解决问题;
解答 解:(1)根据参照线的定义可知,点D(m,n)的所有参照线为:x=m,y=n,y=x+n-m,y=-x+n+m,
故答案为x=m,y=n,y=x+n-m,y=-x+n+m
(2)∵A(6,0),点D在线段OA的垂直平分线上,
∴点D的横坐标为3,
又∵点D有一条参照线是y=-x+7,
∴x=3时,y=-3+7=4,
∴点D坐标为(3,4),
故答案为(3,4).
(3)①如图1中,当点A′在参照线HM上时,设PA=PA′=x.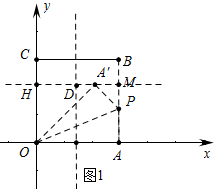
易知OA=OA′=6,OH=4,
∴HA′=$\sqrt{{6}^{2}-{4}^{2}}$=2$\sqrt{5}$,
∴A′M=6-2$\sqrt{5}$,
在Rt△A′PM中,∵A′P2=PM2+A′M2,
∴x2=(4-x)2+(6-2$\sqrt{5}$)2,
∴x=9-3$\sqrt{5}$,
∴P(6,9-3$\sqrt{5}$),
②如图2中,当点A′在参照线DH上时,设PA=PA′=y.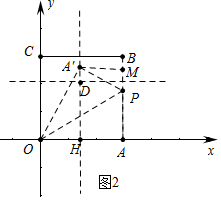
易知A′H=$\sqrt{{6}^{2}-{3}^{2}}$=3$\sqrt{3}$,
在Rt△A′PM中,∵A′P2=PM2+A′M2,
∴y2=32+(3$\sqrt{3}$-y)2,
∴y=2$\sqrt{3}$,
∴P(6,$2\sqrt{3}$),
故答案为(6,2$\sqrt{3}$)或(6,9-3$\sqrt{5}$).
点评 本题考查一次函数综合题、勾股定理、翻折变换、点的“参照线”的定义等知识,解题的关键是理解题意,灵活运用所学知识解决问题,学会用分类讨论的思想思考问题,注意不能漏解.

| x | -2 | 0 | 1 | 3 |
| y | -5 | m | 1 | 5 |
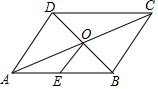 如图,在?ABCD中,对角线AC、BD相交于点O,E为AB的中点,且OE=5,则BC的长为( )
如图,在?ABCD中,对角线AC、BD相交于点O,E为AB的中点,且OE=5,则BC的长为( )| A. | 10 | B. | 9 | C. | 8 | D. | 5 |
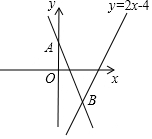 如图,经过点(0,2)的直线y=kx+b与直线y=2x-4相交于点B(1,-2),则不等式2x-4<kx+b<0的解集为$\frac{1}{2}$<x<1.
如图,经过点(0,2)的直线y=kx+b与直线y=2x-4相交于点B(1,-2),则不等式2x-4<kx+b<0的解集为$\frac{1}{2}$<x<1.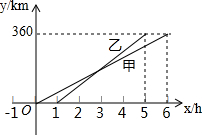 甲、乙两人利用不同的交通工具,沿同一路线从A地出发前往B地,甲出发1h后,y甲、y乙与x之间的函数图象如图所示.
甲、乙两人利用不同的交通工具,沿同一路线从A地出发前往B地,甲出发1h后,y甲、y乙与x之间的函数图象如图所示.
 B.
B.  C.
C.  D.
D. 