题目内容
15.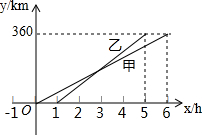 甲、乙两人利用不同的交通工具,沿同一路线从A地出发前往B地,甲出发1h后,y甲、y乙与x之间的函数图象如图所示.
甲、乙两人利用不同的交通工具,沿同一路线从A地出发前往B地,甲出发1h后,y甲、y乙与x之间的函数图象如图所示.(1)甲的速度是60km/h;
(2)当1≤x≤5时,求y乙关于x的函数解析式;
(3)当乙与A地相距240km时,甲与A地相距220km.
分析 (1)根据图象确定出甲的路程与时间,即可求出速度;
(2)利用待定系数法确定出y乙关于x的函数解析式即可;
(3)求出乙距A地240km时的时间,加上1,再乘以甲的速度即可得到结果.
解答 解:(1)根据图象得:甲的速度=360÷6=60km/h,
故答案为:60;
(2)当1≤x≤5时,设y乙=kx+b,
把(1,0)与(5,360)代入得:$\left\{\begin{array}{l}{k+b=0}\\{5k+b=360}\end{array}\right.$,
解得:k=90,b=-90,
∴y乙关于x的函数解析式为y乙=90x-90;
(3)令y乙=90x-90=240,解得x=$\frac{11}{3}$,
∴甲与A地相距:60×$\frac{11}{3}$=220km,
故答案为:220.
点评 此题考查了一次函数的应用以及待定系数法的运用,弄清图象中的数据是解本题的关键.

练习册系列答案
相关题目
3.把直线y=3x向上平移4个单位后所得到直线的函数表达式是( )
| A. | y=3x-4 | B. | y=3x+4 | C. | y=3(x-4) | D. | y=3(x+4) |
20.下列说法中,错误的是( )
| A. | 过两点有且只有一条直线 | |
| B. | 连接两点线段的长度叫两点间的距离 | |
| C. | 等角的补角互余 | |
| D. | 两点之间,线段最短 |
7. 如图,∠3=∠4,则下列结论一定成立的是( )
如图,∠3=∠4,则下列结论一定成立的是( )
 如图,∠3=∠4,则下列结论一定成立的是( )
如图,∠3=∠4,则下列结论一定成立的是( )| A. | AD∥BC | B. | ∠B=∠D | C. | ∠1=∠2 | D. | ∠B+∠BCD=180° |