题目内容
5．
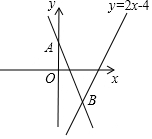如图，经过点（0，2）的直线y=kx+b与直线y=2x-4相交于点B（1，-2），则不等式2x-4＜kx+b＜0的解集为$\frac{1}{2}$＜x＜1．
分析 先利用待定系数法求出直线y=kx+b的解析式为y=-4x+2，再解不等式-4x+2＜0得x＞$\frac{1}{2}$，然后利用函数图象确定2x-4＜kx+b＜0时的自变量的范围．
解答 解：把（0，2）和（1，-2）代入y=kx+b得$\left\{\begin{array}{l}{b=2}\\{k+b=-2}\end{array}\right.$，解得$\left\{\begin{array}{l}{k=-4}\\{b=2}\end{array}\right.$，
所以直线y=kx+b的解析式为y=-4x+2，
解不等式-4x+2＜0得x＞$\frac{1}{2}$，
所以当$\frac{1}{2}$＜x＜1时，2x-4＜kx+b＜0．
故答案为$\frac{1}{2}$＜x＜1．
点评 本题考查了一次函数与一元一次不等式：从函数的角度看，就是寻求使一次函数y=kx+b的值大于（或小于）0的自变量x的取值范围；从函数图象的角度看，就是确定直线y=kx+b在x轴上（或下）方部分所有的点的横坐标所构成的集合．
练习册系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
18．下列图形即是轴对称图形又是中心对称图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |
17．函数y=$\sqrt{x-1}$中，自变量x的取值范围是（ ）
| A． | x≠-1 | B． | x＜1 | C． | x≤1 | D． | x≥1 |
13．分解因式：mx2-8mx+16m，下列结果中正确的是（ ）
| A． | m（x-4）2 | B． | m（x+4）2 | C． | m（x+4）（x-4） | D． | m（x-8）2 |
17．反腐电视剧《人们的名义》正在热播，小明同学在引擎中输入“《人民的名义》”能得到与之相关的结果个数约为2，230，000，这个数用科学记数法表示为（ ）
| A． | 223×104 | B． | 0.223×107 | C． | 2.23×106 | D． | 2.23×107 |
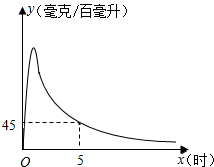如图，实验数据显示，一般成年人喝半斤低度白酒后，1.5时内其血液中酒精含量y（毫克/百毫升）与时间x（时）的关系可以近似的用二次函数y=-200x2+400x刻画，1.5小时后（包括1.5小时）y与x可近似的用反比例函数y=$\frac{k}{x}$（k＞0）刻画．