题目内容
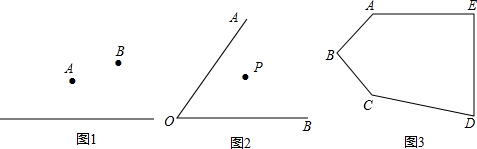
20.(1)如图1,直线同侧有两点A、B,在直线上求一点C,使它到A、B之和最小.(保留作图痕迹不写作法)(2)知识拓展:如图2,点P在∠AOB内部,试在OA、OB上分别找出两点E、F,使△PEF周长最短(保留作图痕迹不写作法)
(3)解决问题:①如图3,在五边形ABCDE中,在BC,DE上分别找一点M,N,使得△AMN周长最小(保留作图痕迹不写作法)
②若∠BAE=125°,∠B=∠E=90°,AB=BC,AE=DE,∠AMN+∠ANM的度数为110°.
分析 (1)根据两点之间线段最短,作A关于直线MN的对称点E,连接BE交直线MN于C,即可得出答案;
(2)作P关于OA、OB的对称点C、D,连接CD角OA、OB于E、F.此时△PEF周长有最小值;
(3)①取点A关于BC的对称点P,关于DE的对称点Q,连接PQ与BC相交于点M,与DE相交于点N,根据轴对称的性质可得AM=PM,AN=QN,然后求出△AMN周长=PQ,根据轴对称确定最短路线问题,PQ的长度即为△AMN的周长最小值;
②根据三角形的内角和等于180°求出∠P+∠Q,再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠AMN=2∠P,∠ANM=2∠Q,然后求解即可得出答案.
解答 解:(1)作A关于直线MN的对称点E,连接BE交直线MN于C,连接AC,BC,
则此时C点符合要求.
(2)作图如下:
(3)①作图如下:
②∵∠BAE=125°,
∴∠P+∠Q=180°-125°=55°,
∵∠AMN=∠P+∠PAM=2∠P,∠ANM=∠Q+∠QAN=2∠Q,
∴∠AMN+∠ANM=2(∠P+∠Q)=2×55°=110°.
点评 此题主要考查了平面内最短路线问题求法以及三角形的外角的性质和垂直平分线的性质等知识,根据已知得出对称点的位置是解题关键.

练习册系列答案
相关题目
5.数据15,18,17,16,17,16,17,15的众数是( )
| A. | 15 | B. | 16 | C. | 17 | D. | 18 |
10.下列方程是二元一次方程的是( )
| A. | x+$\frac{1}{y}$=1 | B. | 2x+3y=6 | C. | x2-y=3 | D. | 3x-5(x+2)=2 |