题目内容
11.先化简(x-$\frac{1}{x}$)÷$\frac{{x}^{2}-2x+1}{{x}^{2}-x}$,然后从-1<x<3的范围内选取一个合适的整数作为x的值代入并求值.分析 根据分式的减法和除法可以化简题目中的式子,然后在-1<x<3中选取一个使得原分式有意义的整数代入化简后的式子即可解答本题.
解答 解:(x-$\frac{1}{x}$)÷$\frac{{x}^{2}-2x+1}{{x}^{2}-x}$
=$\frac{{x}^{2}-1}{x}•\frac{x(x-1)}{(x-1)^{2}}$
=$\frac{(x+1)(x-1)}{x}•\frac{x(x-1)}{(x-1)^{2}}$
=x+1,
∵-1<x<3且x为整数,
∴当x=2时,原式=2+1=3.
点评 本题考查分式的化简求值,解答本题的关键是明确分式化简求值的方法.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.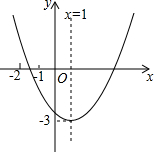 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给下以下结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给下以下结论:
①2a-b=0;
②9a+3b+c<0;
③关于x的一元二次方程ax2+bx+c+3=0有两个相等实数根;
④8a+c<0.
其中正确的个数是( )
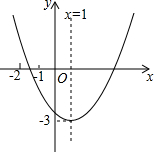 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给下以下结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给下以下结论:①2a-b=0;
②9a+3b+c<0;
③关于x的一元二次方程ax2+bx+c+3=0有两个相等实数根;
④8a+c<0.
其中正确的个数是( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
16.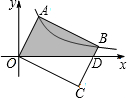 如图,在直角坐标系中,矩形OABC的顶点A、B在双曲线y=$\frac{k}{x}$( x>0)上,BC与x轴交于点D.若点A的坐标为(2,4),则点D的坐标为( )
如图,在直角坐标系中,矩形OABC的顶点A、B在双曲线y=$\frac{k}{x}$( x>0)上,BC与x轴交于点D.若点A的坐标为(2,4),则点D的坐标为( )
 如图,在直角坐标系中,矩形OABC的顶点A、B在双曲线y=$\frac{k}{x}$( x>0)上,BC与x轴交于点D.若点A的坐标为(2,4),则点D的坐标为( )
如图,在直角坐标系中,矩形OABC的顶点A、B在双曲线y=$\frac{k}{x}$( x>0)上,BC与x轴交于点D.若点A的坐标为(2,4),则点D的坐标为( )| A. | ($\frac{22}{3}$,0) | B. | ($\frac{15}{2}$,0) | C. | ($\frac{68}{9}$,0) | D. | ($\frac{48}{5}$,0) |
3.下列运算正确的是( )
| A. | -3a+a=-2a | B. | a6÷a3=a2 | C. | $\sqrt{8}$+$\sqrt{2}$=10 | D. | (-2a2b3)2=4a4b5 |
20.计算a3•(-a)2正确的是( )
| A. | a | B. | -a5 | C. | a6 | D. | a5 |
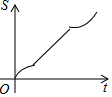
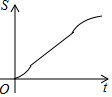
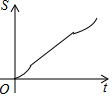
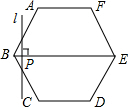 如图,正六边形ABCDEF的边长为6cm,P是对角线BE上一动点,过点P作直线l与BE垂直,动点P从B点出发且以1cm/s的速度匀速平移至E点.设直线l扫过正六边形ABCDEF区域的面积为S(cm2),点P的运动时间为t(s),下列能反映S与t之间函数关系的大致图象是( )
如图,正六边形ABCDEF的边长为6cm,P是对角线BE上一动点,过点P作直线l与BE垂直,动点P从B点出发且以1cm/s的速度匀速平移至E点.设直线l扫过正六边形ABCDEF区域的面积为S(cm2),点P的运动时间为t(s),下列能反映S与t之间函数关系的大致图象是( )