题目内容
19.先化简,再求值:(a+1-$\frac{4a-5}{a-1}$)÷($\frac{1}{a-1}$-$\frac{2}{{a}^{2}-a}$),其中a=2+$\sqrt{2}$.分析 首先对括号内的分式进行通分相加,把除法转化为乘法,然后计算乘法即可化简,最后代入求解即可.
解答 解:原式=$\frac{(a+1)(a-1)-4a+5}{a-1}$÷$\frac{a-2}{a(a-1)}$
=$\frac{(a-2)^{2}}{a-1}$•$\frac{a(a-1)}{a-2}$
=a(a-2).
当a=2+$\sqrt{2}$时,原式=2$\sqrt{2}$+2.
点评 本题考查了分式的化简求值,正确对分式进行通分、约分是关键.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
4.某班抽取6名学生参加体能测试,成绩如下:80,90,75,75,80,80,下列表述错误的是( )
| A. | 平均数是80 | B. | 极差是15 | C. | 中位数是80 | D. | 众数是75 |
8.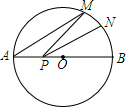 如图,AB是⊙O的直径,AB=8,点M在⊙O上,∠MAB=40°,N是弧MB的中点,P是直径AB上的一动点,PM+PN的最小值为( )
如图,AB是⊙O的直径,AB=8,点M在⊙O上,∠MAB=40°,N是弧MB的中点,P是直径AB上的一动点,PM+PN的最小值为( )
 如图,AB是⊙O的直径,AB=8,点M在⊙O上,∠MAB=40°,N是弧MB的中点,P是直径AB上的一动点,PM+PN的最小值为( )
如图,AB是⊙O的直径,AB=8,点M在⊙O上,∠MAB=40°,N是弧MB的中点,P是直径AB上的一动点,PM+PN的最小值为( )| A. | 4$\sqrt{3}$+1 | B. | 4$\sqrt{3}$ | C. | 4$\sqrt{2}$+1 | D. | 5 |
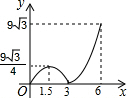
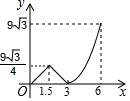
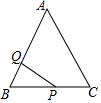 如图,等边△ABC的边长为6,P沿C→B→A运动,Q沿B→A→C运动,且速度都为每秒2个单位,△BPQ面积为y,则y与运动时间x秒的函数的图象大致为( )
如图,等边△ABC的边长为6,P沿C→B→A运动,Q沿B→A→C运动,且速度都为每秒2个单位,△BPQ面积为y,则y与运动时间x秒的函数的图象大致为( )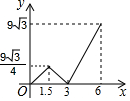
 一次函数y=x+m的图象与反比例函数y=$\frac{k}{x}$的图象交于A、B两点,点A的坐标为(2,1).
一次函数y=x+m的图象与反比例函数y=$\frac{k}{x}$的图象交于A、B两点,点A的坐标为(2,1). 某市为节约水资源,制定了新的居民用水收费标准.按照新标准,用户每月缴纳的水费y(元)与每月用水量x(m3)之间的关系如图所示.
某市为节约水资源,制定了新的居民用水收费标准.按照新标准,用户每月缴纳的水费y(元)与每月用水量x(m3)之间的关系如图所示.