题目内容
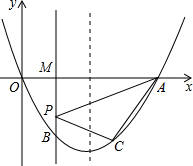 如图,抛物线y=x2-2mx(m>0)与x轴的另一个交点为A,过P(1,-m)作PM⊥x轴于点M,交抛物线于点B.点B关于抛物线对称轴的对称点为C.
如图,抛物线y=x2-2mx(m>0)与x轴的另一个交点为A,过P(1,-m)作PM⊥x轴于点M,交抛物线于点B.点B关于抛物线对称轴的对称点为C.(1)若m=2,求点A和点C的坐标;
(2)令m>1,连接CA,若△ACP为直角三角形,求m的值;
(3)在坐标轴上是否存在点E,使得△PEC是以P为直角顶点的等腰直角三角形?若存在,求出点E的坐标;若不存在,请说明理由.
考点:二次函数综合题
专题:压轴题
分析:(1)令y=0即可求得A点坐标,令x=1求得B点,根据对称轴的性质即可求得C点的坐标.
(2)分别求出PA、PC、AC的平方,根据勾股定理的逆定理即可求得m的值,
(3)先求出PC的斜率,根据互为垂直的两直线的斜率互为负倒数求出直线PE的斜率,然后求出解析式,分别求出与x轴的交点和与y轴的交点,从而求出PE的长,然后判断PE2是否等于PC2即可.
(2)分别求出PA、PC、AC的平方,根据勾股定理的逆定理即可求得m的值,
(3)先求出PC的斜率,根据互为垂直的两直线的斜率互为负倒数求出直线PE的斜率,然后求出解析式,分别求出与x轴的交点和与y轴的交点,从而求出PE的长,然后判断PE2是否等于PC2即可.
解答:解:(1)若m=2,抛物线y=x2-2mx=x2-4x,
∴对称轴x=2,
令y=0,则x2-4x=0,
解得x=0,x=4,
∴A(4,0),
∵P(1,-2),令x=1,则y=-3,
∴B(1,-3),
∴C(3,-3).
(2)∵抛物线y=x2-2mx(m>1),
∴A(2m,0)对称轴x=m,
∵P(1,-m)
把x=1代入抛物线y=x2-2mx,则y=1-2m,
∴B(1,1-2m),
∴C(2m-1,1-2m),
∵PA2=(-m)2+(2m-1)2=5m2-4m+1,
PC2=(2m-2)2+(1-m)2=5m2-10m+5,
AC2=1+(1-2m)2=2-4m+4m2,
∵△ACP为直角三角形,
∴当∠ACP=90°时,PA2=PC2+AC2,
即5m2-4m+1=5m2-10m+5+2-4m+4m2,整理得:4m2-10m+6=0,
解得:m=
,m=1(舍去),
当∠APC=90°时,PA2+PC2=AC2,
即5m2-4m+1+5m2-10m+5=2-4m+4m2,整理得:6m2-10m+4=0,
解得:m=
,m=1,
和1都不符合m>1,
故m=
.
(3)设点F(x,y)是直线PE上任意一点,过点F作FN⊥PM于N,
∵∠FPN=∠PCB,∠PNF=∠CBP=90°,
∴Rt△FNP∽Rt△PBC,
∴NP:NF=BC:BP,即
=
,
∴y=2x-2-m,
∴直线PE的解析式为y=2x-2-m.
令y=0,则x=1+
m,
∴E(1+
m,0),
∴PE2=(-m)2+(
m)2=
,
∴
=5m2-10m+5,解得:m=2,m=
,
∴E(2,0)或E(
,0),
∴在x轴上存在E点,使得△PEC是以P为直角顶点的等腰直角三角形,此时E(2,0)或E(
,0);
令x=0,则y=-2-m,
∴E(0,-2-m)
∴PE2=(-2)2+12=5
∴5m2-10m+5=5,解得m=2,m=0(舍去),
∴E(0,-4)
∴y轴上存在点E,使得△PEC是以P为直角顶点的等腰直角三角形,此时E(0,-4),
∴在坐标轴上是存在点E,使得△PEC是以P为直角顶点的等腰直角三角形,E点的坐标为(2,0)或(
,0)或(0,-4);
∴对称轴x=2,
令y=0,则x2-4x=0,
解得x=0,x=4,
∴A(4,0),
∵P(1,-2),令x=1,则y=-3,
∴B(1,-3),
∴C(3,-3).
(2)∵抛物线y=x2-2mx(m>1),
∴A(2m,0)对称轴x=m,
∵P(1,-m)
把x=1代入抛物线y=x2-2mx,则y=1-2m,
∴B(1,1-2m),
∴C(2m-1,1-2m),
∵PA2=(-m)2+(2m-1)2=5m2-4m+1,
PC2=(2m-2)2+(1-m)2=5m2-10m+5,
AC2=1+(1-2m)2=2-4m+4m2,
∵△ACP为直角三角形,
∴当∠ACP=90°时,PA2=PC2+AC2,
即5m2-4m+1=5m2-10m+5+2-4m+4m2,整理得:4m2-10m+6=0,
解得:m=
| 3 |
| 2 |
当∠APC=90°时,PA2+PC2=AC2,
即5m2-4m+1+5m2-10m+5=2-4m+4m2,整理得:6m2-10m+4=0,
解得:m=
| 2 |
| 3 |
| 2 |
| 3 |
故m=
| 3 |
| 2 |
(3)设点F(x,y)是直线PE上任意一点,过点F作FN⊥PM于N,
∵∠FPN=∠PCB,∠PNF=∠CBP=90°,
∴Rt△FNP∽Rt△PBC,
∴NP:NF=BC:BP,即
| y+m |
| x-1 |
| 2 |
| 1 |
∴y=2x-2-m,
∴直线PE的解析式为y=2x-2-m.
令y=0,则x=1+
| 1 |
| 2 |
∴E(1+
| 1 |
| 2 |
∴PE2=(-m)2+(
| 1 |
| 2 |
| 5m2 |
| 4 |
∴
| 5m2 |
| 4 |
| 2 |
| 3 |
∴E(2,0)或E(
| 4 |
| 3 |
∴在x轴上存在E点,使得△PEC是以P为直角顶点的等腰直角三角形,此时E(2,0)或E(
| 4 |
| 3 |
令x=0,则y=-2-m,
∴E(0,-2-m)
∴PE2=(-2)2+12=5
∴5m2-10m+5=5,解得m=2,m=0(舍去),
∴E(0,-4)
∴y轴上存在点E,使得△PEC是以P为直角顶点的等腰直角三角形,此时E(0,-4),
∴在坐标轴上是存在点E,使得△PEC是以P为直角顶点的等腰直角三角形,E点的坐标为(2,0)或(
| 4 |
| 3 |
点评:本题考查了二次函数的交点的求法,以及直角三角形的判定,等腰直角三角形的判定,勾股定理的应用等.

练习册系列答案
相关题目
若x=2是关于x的方程ax2-bx+2=0的解,则2014-2a+b的值为( )
| A、2012 | B、2013 |
| C、2015 | D、2016 |
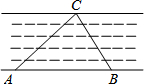 如图,为了测量不能到达对岸的河宽,在河的岸边选两点A、B,测得AB=100米,分别在A点和B点看对岸一点C,测得∠A=43°,∠B=65°,求河宽(河宽可看成是点C到直线AB的距离).
如图,为了测量不能到达对岸的河宽,在河的岸边选两点A、B,测得AB=100米,分别在A点和B点看对岸一点C,测得∠A=43°,∠B=65°,求河宽(河宽可看成是点C到直线AB的距离). 如图,将一矩形OABC放在直角坐标系中,O为坐标原点,点A在y轴正半轴上,OA=2,OC=4,过点E的反比例函数y=
如图,将一矩形OABC放在直角坐标系中,O为坐标原点,点A在y轴正半轴上,OA=2,OC=4,过点E的反比例函数y= 如图,左边是一个由5个棱长为1的小正方体组合而成的几何图,现在增加一个小正方体,使其主视图如右,则增加后的几何体的左视图的面积为
如图,左边是一个由5个棱长为1的小正方体组合而成的几何图,现在增加一个小正方体,使其主视图如右,则增加后的几何体的左视图的面积为