题目内容
在综合实践活动课中,王老师出了这样一道题:
如图1,在矩形ABCD中,M是BC的中点,过点M作ME∥AC交BD于点E,作MF∥BD交AC于点F.求证:四边形OEMF是菱形.
做完题后,同学们按照老师的要求进行变式或拓展,提出新的问题让其它同学解答.
(1)小明同学说:“我把条件中的‘矩形ABCD’改为‘菱形ABCD’,如图2所示,发现四边形OEMF是矩形.”请给予证明;
(2)小芳同学说:“我把条件中的‘点M是BC的中点’改为‘点M是BC延长线上的一个动点’,发现点F落在AC的延长线上,如图3所示,此时OB、ME、MF三条线段之间存在某种数量关系.”请你写出这个结论,并说明理由.
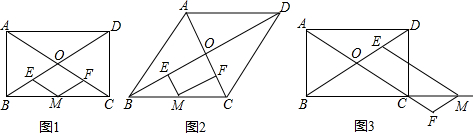
如图1,在矩形ABCD中,M是BC的中点,过点M作ME∥AC交BD于点E,作MF∥BD交AC于点F.求证:四边形OEMF是菱形.
做完题后,同学们按照老师的要求进行变式或拓展,提出新的问题让其它同学解答.
(1)小明同学说:“我把条件中的‘矩形ABCD’改为‘菱形ABCD’,如图2所示,发现四边形OEMF是矩形.”请给予证明;
(2)小芳同学说:“我把条件中的‘点M是BC的中点’改为‘点M是BC延长线上的一个动点’,发现点F落在AC的延长线上,如图3所示,此时OB、ME、MF三条线段之间存在某种数量关系.”请你写出这个结论,并说明理由.

考点:四边形综合题
专题:
分析:(1)首先证得四边形OEMF是平行四边形,然后利用菱形的对角线互相垂直证得∠EOF=90°,利用有一个角是直角的平行四边形是矩形证得结论;
(2)根据四边形OEMF是平行四边形,得到OE=MF,根据四边形ABCD是矩形,得到OB=
BD,OC=
AD,且AC=BD,从而得到OB=OC,进一步得到BE=ME,从而证得结论OB=BE-OE=ME-MF.
(2)根据四边形OEMF是平行四边形,得到OE=MF,根据四边形ABCD是矩形,得到OB=
| 1 |
| 2 |
| 1 |
| 2 |
解答:(1)证明:∵ME∥AC,MF∥BD,
∴四边形OEMF是平行四边形.
又∵四边形ABCD是菱形,
∴AC⊥BD,即∠EOF=90°,
∴四边形OEMF是矩形.
(2)结论:OB=ME-MF.
理由如下:∵ME∥AC,MF∥BD,
∴四边形OEMF 是平行四边形,
∴OE=MF,
又∵四边形ABCD是矩形,
∴OB=
BD,OC=
AD,且AC=BD,
∴OB=OC,
∴∠OBC=∠OCB,
由ME∥AC可知,∠OCB=∠EMB,
∴BE=ME,
∴OB=BE-OE=ME-MF.
∴四边形OEMF是平行四边形.
又∵四边形ABCD是菱形,
∴AC⊥BD,即∠EOF=90°,
∴四边形OEMF是矩形.
(2)结论:OB=ME-MF.
理由如下:∵ME∥AC,MF∥BD,
∴四边形OEMF 是平行四边形,
∴OE=MF,
又∵四边形ABCD是矩形,
∴OB=
| 1 |
| 2 |
| 1 |
| 2 |
∴OB=OC,
∴∠OBC=∠OCB,
由ME∥AC可知,∠OCB=∠EMB,
∴BE=ME,
∴OB=BE-OE=ME-MF.
点评:本题考查了矩形的性质及判断、菱形的性质、平行四边形的性质及判定,涉及的知识点比较多,较复杂,但难度不算很大.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若等腰三角形的两边是方程x2-6x+8=0的两根,则此三角形的周长为( )
| A、8 | B、10 |
| C、8或10 | D、6或8 |
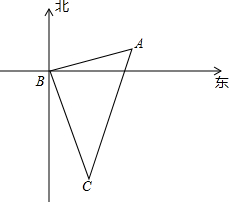 马航事件牵动了全国甚至全世界人们的心,当得知MH370客机最后失
马航事件牵动了全国甚至全世界人们的心,当得知MH370客机最后失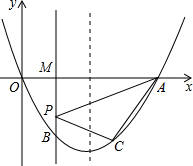 如图,抛物线y=x2-2mx(m>0)与x轴的另一个交点为A,过P(1,-m)作PM⊥x轴于点M,交抛物线于点B.点B关于抛物线对称轴的对称点为C.
如图,抛物线y=x2-2mx(m>0)与x轴的另一个交点为A,过P(1,-m)作PM⊥x轴于点M,交抛物线于点B.点B关于抛物线对称轴的对称点为C.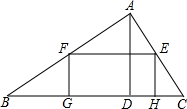 如图,有一块三角形废料,AD是Rt△ABC的高,∠BAC=90°,AD⊥BC,现为了充分利用,要用这块废料切出一个矩形EFGH.点G、H在BC边上,点F在AB边上,点E在AC边上,AC=6,AB=8.
如图,有一块三角形废料,AD是Rt△ABC的高,∠BAC=90°,AD⊥BC,现为了充分利用,要用这块废料切出一个矩形EFGH.点G、H在BC边上,点F在AB边上,点E在AC边上,AC=6,AB=8. 某校男子足球队的年龄分布如图的条形图,请求出这些队员年龄的平均数、众数、中位数.
某校男子足球队的年龄分布如图的条形图,请求出这些队员年龄的平均数、众数、中位数.