题目内容
6.计算:sin30°cot260°+$\sqrt{2}$sin45°-°$\frac{tan45°}{\sqrt{3}tan60°}$.分析 原式利用特殊角的三角函数值计算即可得到结果.
解答 解:原式=$\frac{1}{2}$×$\frac{1}{3}$+$\sqrt{2}$×$\frac{\sqrt{2}}{2}$-$\frac{1}{\sqrt{3}×\sqrt{3}}$=$\frac{1}{6}$+1-$\frac{1}{3}$=$\frac{5}{6}$.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.二次函数y=ax2+bx+c的部分对应值如下表:
当x=-1时,对应的函数值y=-22.
| x | … | -3 | -2 | 0 | 1 | 3 | 5 | … |
| y | … | -54 | -36 | -12 | -6 | -6 | -22 | … |
15.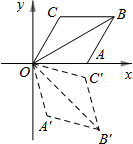 如图,已知菱形OABC的一边OA在x轴上,OA∥BC,OC∥AB,且OA=AB=BC=CO,将菱形OABC变换到菱形OA′B′C′的位置,若OB=OB′=2$\sqrt{3}$,∠C=120°,∠BOB′=75°,则点B′的坐标为( )
如图,已知菱形OABC的一边OA在x轴上,OA∥BC,OC∥AB,且OA=AB=BC=CO,将菱形OABC变换到菱形OA′B′C′的位置,若OB=OB′=2$\sqrt{3}$,∠C=120°,∠BOB′=75°,则点B′的坐标为( )
 如图,已知菱形OABC的一边OA在x轴上,OA∥BC,OC∥AB,且OA=AB=BC=CO,将菱形OABC变换到菱形OA′B′C′的位置,若OB=OB′=2$\sqrt{3}$,∠C=120°,∠BOB′=75°,则点B′的坐标为( )
如图,已知菱形OABC的一边OA在x轴上,OA∥BC,OC∥AB,且OA=AB=BC=CO,将菱形OABC变换到菱形OA′B′C′的位置,若OB=OB′=2$\sqrt{3}$,∠C=120°,∠BOB′=75°,则点B′的坐标为( )| A. | (3,$\sqrt{3}$) | B. | (3,-$\sqrt{3}$) | C. | ($\sqrt{6}$,$\sqrt{6}$) | D. | ($\sqrt{6}$,-$\sqrt{6}$) |
20.一辆列车通过隧道,从车头进车尾出隧道共用1分30秒,已知列车的速度为100千米/时,列车长100米.则隧道长为( )
| A. | 2.5千米 | B. | 1.5千米 | C. | 2.4千米 | D. | 14.9千米 |
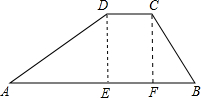 如图,水库大坝的横断面是梯形,坝顶宽是8m,坝高为30m.斜坡AD的坡度为i=$\sqrt{3}$:3,斜坡CB的坡度为i=2:3.求斜坡AD的坡角α,坝度宽AB和斜坡AD的长.
如图,水库大坝的横断面是梯形,坝顶宽是8m,坝高为30m.斜坡AD的坡度为i=$\sqrt{3}$:3,斜坡CB的坡度为i=2:3.求斜坡AD的坡角α,坝度宽AB和斜坡AD的长.