题目内容
17.(1)计算:(3-$\sqrt{7}$)(3+$\sqrt{7}$)+$\sqrt{2}$(2-$\sqrt{2}$)(2)解方程:$\frac{x-3}{x-2}$+1=$\frac{3}{2-x}$.
分析 (1)利用平方差公式进行计算,并化简即可;
(2)先去分母方程的两边同时乘以x-2,解方程,并进行检验.
解答 解:(1)计算:(3-$\sqrt{7}$)(3+$\sqrt{7}$)+$\sqrt{2}$(2-$\sqrt{2}$),
=9-7+2$\sqrt{2}$-2,
=2$\sqrt{2}$;
(2)解方程:$\frac{x-3}{x-2}$+1=$\frac{3}{2-x}$,
去分母得:x-3+x-2=-3,
2x=2,
x=1,
检验:当x=1时,x-2=1-2≠0,
∴x=1是原方程的解.
点评 本题考查了二次根式的混合计算以及解分式方程,正确化简是解题的关键,注意分式方程最后要检验.

练习册系列答案
相关题目
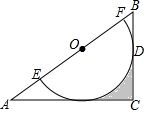 如图,在Rt△ABC中,∠C=90°,O为AB边上一点,⊙O交AB于E,F两点,BC切⊙O于点D,且CD=$\frac{1}{2}$EF=1.
如图,在Rt△ABC中,∠C=90°,O为AB边上一点,⊙O交AB于E,F两点,BC切⊙O于点D,且CD=$\frac{1}{2}$EF=1. 如图,AB=AC,点D,E分别在AB,AC上,请添加一个条件BD=EC或∠B=∠C,即可推出OD=OE.
如图,AB=AC,点D,E分别在AB,AC上,请添加一个条件BD=EC或∠B=∠C,即可推出OD=OE.