题目内容
【问题背景】
如图1:在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E、F分别是BC、CD上的点,且∠EAF=60°,试探究图中线段BE、EF、FD之间的数量关系.
小王同学探究此问题的方法是:延长FD到点G,使DG=BE,连结AG,先证明△ABE≌△ADG,再证明△AEF≌△GF,可得出结论,他的结论应是 .
【探索延伸】如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是BC,CD上的点,且∠EAF=
∠BAD,上述结论是否仍然成立,并说明理由.
【学以致用】
如图3,四边形ABCD是边长为5的正方形,∠EBF=45°,直接写出△DEF的周长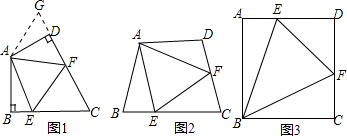 .
.
如图1:在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E、F分别是BC、CD上的点,且∠EAF=60°,试探究图中线段BE、EF、FD之间的数量关系.
小王同学探究此问题的方法是:延长FD到点G,使DG=BE,连结AG,先证明△ABE≌△ADG,再证明△AEF≌△GF,可得出结论,他的结论应是
【探索延伸】如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是BC,CD上的点,且∠EAF=
| 1 |
| 2 |
【学以致用】
如图3,四边形ABCD是边长为5的正方形,∠EBF=45°,直接写出△DEF的周长
 .
.考点:全等三角形的判定与性质
专题:
分析:(1)延长FD到点G.使DG=BE.连结AG,即可证明△ABE≌△ADG,可得AE=AG,再证明△AEF≌△AGF,可得EF=FG,即可解题;
(2)延长FD到点G.使DG=BE.连结AG,即可证明△ABE≌△ADG,可得AE=AG,再证明△AEF≌△AGF,可得EF=FG,即可解题;
(3)延长DC,截取CG=AE,连接BG,根据SAS定理可得出△AEB≌△CGB,故可得出BE=BG,∠ABE=∠CBG,再由∠EBF=45°,∠ABC=90°可得出∠ABE+∠CBF=45°,故∠CBF+∠CBG=45°,由SAS定理可得△EBF≌△GBF,故EF=GF,故△DEF的周长=EF+ED+CF=AE+CF+DE+DF=AD+CD,由此可得出结论.
(2)延长FD到点G.使DG=BE.连结AG,即可证明△ABE≌△ADG,可得AE=AG,再证明△AEF≌△AGF,可得EF=FG,即可解题;
(3)延长DC,截取CG=AE,连接BG,根据SAS定理可得出△AEB≌△CGB,故可得出BE=BG,∠ABE=∠CBG,再由∠EBF=45°,∠ABC=90°可得出∠ABE+∠CBF=45°,故∠CBF+∠CBG=45°,由SAS定理可得△EBF≌△GBF,故EF=GF,故△DEF的周长=EF+ED+CF=AE+CF+DE+DF=AD+CD,由此可得出结论.
解答: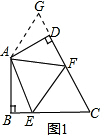 (1)解:如图1,
(1)解:如图1,
在△ABE和△ADG中,
∵
,
∴△ABE≌△ADG(SAS),
∴AE=AG,∠BAE=∠DAG,
∵∠EAF=
∠BAD,
∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD-∠EAF=∠EAF,
∴∠EAF=∠GAF,
在△AEF和△GAF中,
∵
,
∴△AEF≌△AGF(SAS),
∴EF=FG,
∵FG=DG+DF=BE+DF,
∴EF=BE+DF;
故答案为:EF=BE+DF.
(2)解:结论EF=BE+DF仍然成立;
理由:如图2,延长FD到点G.使DG=BE.连结AG,
在△ABE和△ADG中,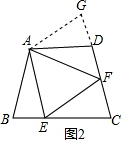
∵
,
∴△ABE≌△ADG(SAS),
∴AE=AG,∠BAE=∠DAG,
∵∠EAF=
∠BAD,
∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD-∠EAF=∠EAF,
∴∠EAF=∠GAF,
在△AEF和△GAF中,
∵
,
∴△AEF≌△AGF(SAS),
∴EF=FG,
∵FG=DG+DF=BE+DF,
∴EF=BE+DF;
(3)解:如图3,延长DC到点G,截取CG=AE,连接BG,
在△AEB与△CGB中,
∵
,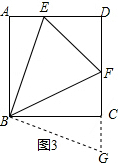
∴△AEB≌△CGB(SAS),
∴BE=BG,∠ABE=∠CBG.
∵∠EBF=45°,∠ABC=90°,
∴∠ABE+∠CBF=45°,
∴∠CBF+∠CBG=45°.
在△EBF与△GBF中,
∵
,
∴△EBF≌△GBF(SAS),
∴EF=GF,
∴△DEF的周长=EF+ED+CF=AE+CF+DE+DF=AD+CD=4+4=8.
 (1)解:如图1,
(1)解:如图1,在△ABE和△ADG中,
∵
|
∴△ABE≌△ADG(SAS),
∴AE=AG,∠BAE=∠DAG,
∵∠EAF=
| 1 |
| 2 |
∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD-∠EAF=∠EAF,
∴∠EAF=∠GAF,
在△AEF和△GAF中,
∵
|
∴△AEF≌△AGF(SAS),
∴EF=FG,
∵FG=DG+DF=BE+DF,
∴EF=BE+DF;
故答案为:EF=BE+DF.
(2)解:结论EF=BE+DF仍然成立;
理由:如图2,延长FD到点G.使DG=BE.连结AG,
在△ABE和△ADG中,

∵
|
∴△ABE≌△ADG(SAS),
∴AE=AG,∠BAE=∠DAG,
∵∠EAF=
| 1 |
| 2 |
∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD-∠EAF=∠EAF,
∴∠EAF=∠GAF,
在△AEF和△GAF中,
∵
|
∴△AEF≌△AGF(SAS),
∴EF=FG,
∵FG=DG+DF=BE+DF,
∴EF=BE+DF;
(3)解:如图3,延长DC到点G,截取CG=AE,连接BG,
在△AEB与△CGB中,
∵
|

∴△AEB≌△CGB(SAS),
∴BE=BG,∠ABE=∠CBG.
∵∠EBF=45°,∠ABC=90°,
∴∠ABE+∠CBF=45°,
∴∠CBF+∠CBG=45°.
在△EBF与△GBF中,
∵
|
∴△EBF≌△GBF(SAS),
∴EF=GF,
∴△DEF的周长=EF+ED+CF=AE+CF+DE+DF=AD+CD=4+4=8.
点评:本题考查的是全等三角形的判定与性质,根据题意作出辅助线,构造出全等三角形是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列事件中,必然事件是( )
| A、抛掷1个均匀的骰子,出现6点向上 |
| B、两直线被第三条直线所截,同位角相等 |
| C、366人中至少有2人的生日相同 |
| D、实数的绝对值是非负数 |
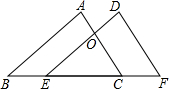 已知,如图,点B、E、C、F四点在同一条直线上,AB∥DE,AB=DE,AC、DE相交于点O,BE=CF.求证:AC=DF.
已知,如图,点B、E、C、F四点在同一条直线上,AB∥DE,AB=DE,AC、DE相交于点O,BE=CF.求证:AC=DF.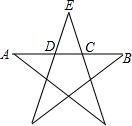 如图,在五角星图形中,AD=BC,C,D两点都是AB的黄金分割点,AB=1,求CD的长.
如图,在五角星图形中,AD=BC,C,D两点都是AB的黄金分割点,AB=1,求CD的长.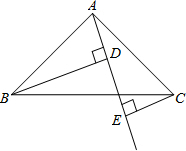 如图,已知△ABC中,∠BAC=90°,AB=AC,AE是过点A的一条直线,且B点和C点在AE的两侧,BD⊥AE于点D,CE⊥AE于点E.
如图,已知△ABC中,∠BAC=90°,AB=AC,AE是过点A的一条直线,且B点和C点在AE的两侧,BD⊥AE于点D,CE⊥AE于点E. 如图,将甲图经过
如图,将甲图经过