如图:两个同心圆.其中大圆的弦AD交小圆于C.D两点那么:AB与CD相等吗?为什么? 题目和参考答案——青夏教育精英家教网——

题目内容

18．

如图：两个同心圆，其中大圆的弦AD交小圆于C、D两点那么：AB与CD相等吗？为什么？

分析过点O作OE⊥AD于点E，由垂径定理即可得出结论．

解答解：相等．
理由：过点O作OE⊥AD于点E，
∵AD是大圆的弦，BC是小圆的弦，
∴AE=DE，BE=CE，
∴AE-BE=DE-CE，即AB=CD．

点评本题考查的是垂径定理，熟知平分弦的直径平分这条弦，并且平分弦所对的两条弧是解答此题的关键．

练习册系列答案

好学生课堂达标系列答案

随堂10分钟系列答案

集优方案系列答案

仁爱英语同步练习册系列答案

巴蜀学案同步导学系列答案

填充图册中国地图出版社系列答案

第1考卷课时卷系列答案

学习实践园地系列答案

书立方吉林专版系列答案

奇迹课堂系列答案

相关题目

11．解方程：
①（x+1）²-144=0；
②x²+2x-5=0；
③（x-3）²+2x（x-3）=0；
④（x+1）（x+8）=-12．

9．等腰三角形的底角为80°，则它的顶角是（　　）

6．若多项式x²+kx+25是一个多项式的平方，则k=±10．

13．直线y=$\frac{1}{2}$x+2与x轴，y轴分别相交于A、B两点，与反比例函数y=$\frac{k}{x}$（x＞0）的图象相交于点C（2，3）．点P是反比例函数图象上一点，作PE垂直x轴于E，若以P、O、E为顶点的三角形与△AOB相似，则点P的坐标是（2$\sqrt{3}$，$\sqrt{3}$），（$\sqrt{3}$，2$\sqrt{3}$）．

3．（2×10²）²=4×10⁴；（-3×10³）³=-27×10⁹．

10．反比例函数$y=-\frac{2}{x}$图象上有三点$A（-\frac{1}{2}，{y_1}）$、B（-1，y₂）、$B（\frac{1}{3}，{y_3}）$，则y₁、y₂、y₃的大小关系是（　　）

y₁＜y₂＜y₃

y₂＜y₁＜y₃

y₃＜y₁＜y₂

y₃＜y₂＜y₁

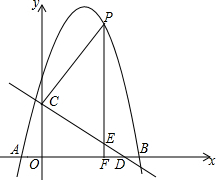如图，抛物线y=-x²+bx+c与x轴交于A（-1，0），B（5，0）两点，直线y=-$\frac{3}{4}$x+3与y轴交于点C，与x轴交于点D．点P是x轴上方的抛物线上一动点，过点P作PF⊥x轴于点F，交直线CD于点E．设点P的横坐标为m．
（1）求抛物线的解析式；
（2）若PE=5EF，求m的值．

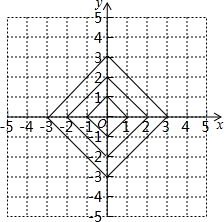在平面直角坐标系中，横坐标、纵坐标都为整数的点称为整点，如图，由里向外数的第2各正方形开始，分别是由第1个正方形各顶点的横坐标和纵坐标分别乘1，2，3，…得到的，请你观察图形，猜想由里向外第12个正方形四条边上的整点个数为48．