题目内容
13.数学老师布置了一道思考题:“计算(-$\frac{1}{30}$)÷($\frac{2}{3}$-$\frac{1}{10}$+$\frac{1}{6}$-$\frac{2}{5}$)”,小红和小明两位同学经过仔细思考,用不同的方法解答了这个问题.小红的解法:原式的倒数为($\frac{2}{3}$-$\frac{1}{10}$+$\frac{1}{6}$-$\frac{2}{5}$)÷(-$\frac{1}{30}$)=($\frac{2}{3}$-$\frac{1}{10}$+$\frac{1}{6}$-$\frac{2}{5}$)×(-30)=-20+3-5+12=-10.所以(-$\frac{1}{30}$)÷($\frac{2}{3}$-$\frac{1}{10}$+$\frac{1}{6}$-$\frac{2}{5}$)=-$\frac{1}{10}$.
小明的解法:原式=(-$\frac{1}{30}$)÷[($\frac{2}{3}$+$\frac{1}{6}$)-($\frac{1}{10}$+$\frac{2}{5}$)]=(-$\frac{1}{30}$)÷($\frac{5}{6}$-$\frac{1}{2}$)=-$\frac{1}{30}$×3=-$\frac{1}{10}$.
请你分别用小红和小明的方法计算:(-$\frac{1}{42}$)÷($\frac{1}{6}$-$\frac{3}{14}$+$\frac{2}{3}$-$\frac{2}{7}$).
分析 原式分别利用小红与小明的解法计算即可.
解答 解:法1:原式的倒数为($\frac{1}{6}$-$\frac{3}{14}$+$\frac{2}{3}$-$\frac{2}{7}$)÷(-$\frac{1}{42}$)=($\frac{1}{6}$-$\frac{3}{14}$+$\frac{2}{3}$-$\frac{2}{7}$)×(-42)=-7+9-28+12=-35+21=-14,
∴(-$\frac{1}{42}$)÷($\frac{1}{6}$-$\frac{3}{14}$+$\frac{2}{3}$-$\frac{2}{7}$)=-$\frac{1}{14}$;
法2:原式=(-$\frac{1}{42}$)÷[($\frac{1}{6}$+$\frac{2}{3}$)-($\frac{3}{14}$+$\frac{2}{7}$)]=-$\frac{1}{42}$÷($\frac{5}{6}$-$\frac{1}{2}$)=-$\frac{1}{42}$÷$\frac{1}{3}$=-$\frac{1}{42}$×3=-$\frac{1}{14}$.
点评 此题考查了有理数的混合运算,以及倒数,熟练掌握运算法则是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.已知⊙A在平面直角坐标系中,点A的坐标为(-7,0),点B的坐标为(-7,4),点C的坐标为(-12,0),若⊙A的半径为5,则下列说法中不正确的是( )
| A. | 点B在⊙A内 | B. | 点C在⊙A上 | C. | y轴和⊙A相切 | D. | x轴和⊙A相交 |
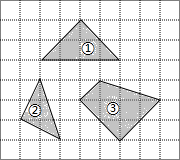 如图,在正方形网格中,每个小正方形的边长均相等,网格中三个多边形(分别标记为①,②,③)的顶点均在格点上,被一个多边形覆盖的网格线中,竖直部分线段长度之和记为m,水平部分线段长度之和记为n,则这三个多边形中满足m=n的是②③.
如图,在正方形网格中,每个小正方形的边长均相等,网格中三个多边形(分别标记为①,②,③)的顶点均在格点上,被一个多边形覆盖的网格线中,竖直部分线段长度之和记为m,水平部分线段长度之和记为n,则这三个多边形中满足m=n的是②③.