题目内容
3.己知二次函数y=ax2-ax-x(a≠0)(1)若对称轴是直线x=1
①求二次函数的解析式;
②二次函数y=ax2-ax-x-t(t为实数)图象的顶点在x轴上,求t的值;
(2)把抛物线k1:y=ax2-ax-x向上平移1个单位得到新的抛物线k2,若a<0,求k2落在x轴上方的部分对应的x的取值范围.
分析 (1)①由对称轴是直线x=1,得到-$\frac{-(a+1)}{a}$=1,于是得到结论;②∵二次函数y=$\frac{1}{2}$x2-$\frac{3}{2}$x-t(t为实数)图象的顶点在x轴上,列方程得到t=-$\frac{9}{8}$;
(2)由y=ax2-ax-x向上平移1个单位得到新的抛物线k2,得到新的抛物线k2的解析式为y=ax2-ax-x+1,解方程得到x1=1,x2=$\frac{1}{a}$,于是得到结论.
解答 解:(1)①∵对称轴是直线x=1,
∴-$\frac{-(a+1)}{a}$=1,
∴a=$\frac{1}{2}$,
∴二次函数的解析式为:y=$\frac{1}{2}$x2-$\frac{3}{2}$x;
②∵二次函数y=$\frac{1}{2}$x2-$\frac{3}{2}$x-t(t为实数)图象的顶点在x轴上,
∴(-$\frac{3}{2}$)2+4×$\frac{1}{2}$t=0,
∴t=-$\frac{9}{8}$;
(2)∵y=ax2-ax-x向上平移1个单位得到新的抛物线k2,
∴新的抛物线k2的解析式为y=ax2-ax-x+1,
∴当y=0时,ax2-ax-x+1=0,
解得:x1=1,x2=$\frac{1}{a}$,
∴k2落在x轴上方的部分对应的x的取值范围:$\frac{1}{a}$<x<1.
点评 本题考查了抛物线与x轴的交点,二次函数的图象与几何变换,求二次函数的解析式,正确的理解题意是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.不等式3x-1≤2(x+2)的正整数解有几个( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
13.若(x+a)(x-b)=x2+mx+n,则m,n的值分别是( )
| A. | m=a-b,n=ab | B. | m=-(a-b),n=ab | C. | m=a-b,n=-ab | D. | m=-(a-b),n=-ab |
 如图,在△ABC中,D、E、F分别是各边的中点,AH是高,∠DHF=50°,∠DAF=50°.
如图,在△ABC中,D、E、F分别是各边的中点,AH是高,∠DHF=50°,∠DAF=50°.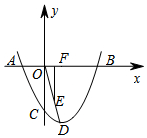 如图,一抛物线经过点A(-2,0),B(6,0),C(0,-3),D为抛物线的顶点,过OD的中点E,作EF⊥x轴于点F,G为x轴上一动点,M为抛物线上一动点,N为直线EF上一动点,当以F、G、M、N为顶点的四边形是正方形时,点G的坐标为(4-2$\sqrt{6}$,0)、(-4,0)、(4+2$\sqrt{6}$,0)或(4,0).
如图,一抛物线经过点A(-2,0),B(6,0),C(0,-3),D为抛物线的顶点,过OD的中点E,作EF⊥x轴于点F,G为x轴上一动点,M为抛物线上一动点,N为直线EF上一动点,当以F、G、M、N为顶点的四边形是正方形时,点G的坐标为(4-2$\sqrt{6}$,0)、(-4,0)、(4+2$\sqrt{6}$,0)或(4,0).