题目内容
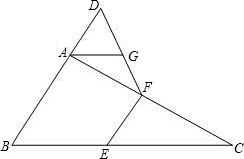 如图,△ABC中,∠BAC=90°,延长BA至D,使AD=
如图,△ABC中,∠BAC=90°,延长BA至D,使AD=| 1 |
| 2 |
(1)判断四边形DBEF的形状并证明;
(2)过点A作AG⊥BC交DF于G,求证:AG=DG.
考点:等腰梯形的判定,三角形中位线定理,等腰梯形的性质
专题:
分析:(1)利用梯形的判定首先得出四边形DBEF为梯形,进而得出四边形HFEB是平行四边形,得出BE=FD进而得出答案;
(2)利用四边形DBEF为等腰梯形,得出∠B=∠D,利用AG∥BG,∠B=∠DAG,得出答案.
(2)利用四边形DBEF为等腰梯形,得出∠B=∠D,利用AG∥BG,∠B=∠DAG,得出答案.
解答: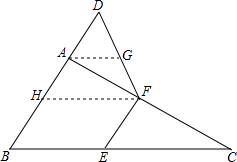 (1)解:四边形DBEF为等腰梯形,
(1)解:四边形DBEF为等腰梯形,
理由如下:
如图,过点F作FH∥BC,交AB于点H,
∵FH∥BC,点F是AC的中点,点E是BC的中点,
∴AH=BH=
AB,EF∥AB,
显然EF<AB<AD,∴EF≠AD,
∴四边形DBEF为梯形,
∵AD=
AB,
∴AD=AH,
∵CA⊥AB,
∴CA是DH的中垂线,
∴DF=FH,
∵FH∥BC,EF∥AB,
∴四边形HFEB是平行四边形,
∴FH=BE,
∴BE=FD,
故四边形DBEF为等腰梯形;
(2)证明:∵四边形DBEF为等腰梯形,
∴∠B=∠D,
∵AG∥BG,∠B=∠DAG,
∴∠D=∠DAG,
∴AG=DG.
 (1)解:四边形DBEF为等腰梯形,
(1)解:四边形DBEF为等腰梯形,理由如下:
如图,过点F作FH∥BC,交AB于点H,
∵FH∥BC,点F是AC的中点,点E是BC的中点,
∴AH=BH=
| 1 |
| 2 |
显然EF<AB<AD,∴EF≠AD,
∴四边形DBEF为梯形,
∵AD=
| 1 |
| 2 |
∴AD=AH,
∵CA⊥AB,
∴CA是DH的中垂线,
∴DF=FH,
∵FH∥BC,EF∥AB,
∴四边形HFEB是平行四边形,
∴FH=BE,
∴BE=FD,
故四边形DBEF为等腰梯形;
(2)证明:∵四边形DBEF为等腰梯形,
∴∠B=∠D,
∵AG∥BG,∠B=∠DAG,
∴∠D=∠DAG,
∴AG=DG.
点评:此题主要考查了等腰梯形的判定以及其性质和平行四边形的判定与性质等知识,得出BE=FD是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知线段AB⊥x轴,且AB=4,若点A坐标为(-2,3),则点B坐标( )
| A、(-2,7) |
| B、(2,3) |
| C、(2,3)或(-6,3) |
| D、(-2,7)或(-2,-1) |
 如图所示,已知CE∥BD,∠C=∠D,证明:∠A=∠F.
如图所示,已知CE∥BD,∠C=∠D,证明:∠A=∠F.