题目内容
 如图,一张圆心角为45°的扇形纸板按如图方式剪得一个正方形,正方形的边长为1,则扇形纸板的面积是
如图,一张圆心角为45°的扇形纸板按如图方式剪得一个正方形,正方形的边长为1,则扇形纸板的面积是考点:扇形面积的计算,勾股定理,正方形的性质
专题:
分析:连接OC,则△OAB是等腰直角三角形,然后利用勾股定理即可求得半径OC的长,然后利用扇形的面积公式求解.
解答: 解:连接OC.
解:连接OC.
∵四边形ABCD是正方形,
∴∠OAB=90°,
又∵∠AOB=45°,
∴△OAB是等腰直角三角形,
∴OA=AB=1,则OD=2,
在直角△OCD中,OC=
=
=
,
则扇形纸板的面积是:
=
π.
故答案是:
π.
 解:连接OC.
解:连接OC.∵四边形ABCD是正方形,
∴∠OAB=90°,
又∵∠AOB=45°,
∴△OAB是等腰直角三角形,
∴OA=AB=1,则OD=2,
在直角△OCD中,OC=
| AD2+CD2 |
| 22+12 |
| 5 |
则扇形纸板的面积是:
45π(
| ||
| 360 |
| 5 |
| 8 |
故答案是:
| 5 |
| 8 |
点评:本题考查了勾股定理和扇形的面积公式,正确求得圆的半径OC的长是关键.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
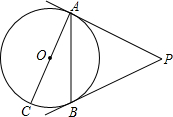 如图,PA、PB是⊙O的切线,A、B为切点,AC是⊙O的直径,AC=6,∠P=50°,求:
如图,PA、PB是⊙O的切线,A、B为切点,AC是⊙O的直径,AC=6,∠P=50°,求:

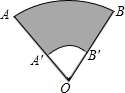 如图所示是两个同心圆被其两条半径所截得到的图形,已知
如图所示是两个同心圆被其两条半径所截得到的图形,已知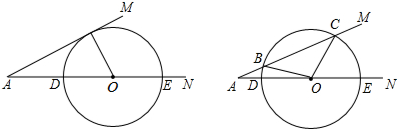
 如图,D为以AB为直径的半圆上的中点,C为AD弧上的点,弦BC、AD相交于点E,弦AC、BD的延长线相交于点F,求证:DE=DF.
如图,D为以AB为直径的半圆上的中点,C为AD弧上的点,弦BC、AD相交于点E,弦AC、BD的延长线相交于点F,求证:DE=DF.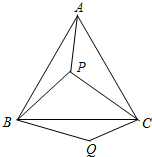 如图,P是等边三角形ABC内的一点,连结PA,PB,PC,以BP为边作∠PBQ=60°,且BP=BQ,连结CQ.
如图,P是等边三角形ABC内的一点,连结PA,PB,PC,以BP为边作∠PBQ=60°,且BP=BQ,连结CQ.