题目内容
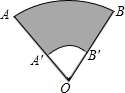 如图所示是两个同心圆被其两条半径所截得到的图形,已知
如图所示是两个同心圆被其两条半径所截得到的图形,已知 |
| AB |
 |
| A′B′ |
(1)∠O=
| l-l′ |
| d |
| 180 |
| π |
(2)SABB′A′=
| 1 |
| 2 |
考点:扇形面积的计算,弧长的计算
专题:
分析:(1)设∠O=n°,则
的长和
的长即可求得,然后根据OA-OA'=d,即可求解;
(2)根据SABB′A′=S扇形OAB-S扇形OA'B'即可证得.
 |
| AB |
 |
| A′B′ |
(2)根据SABB′A′=S扇形OAB-S扇形OA'B'即可证得.
解答:证明:(1)设∠O=n°,则
的长为l=
,
的长为l′=
,
则OA=
,OA'=
,
∵OA-OA'=d,
则
-
=d,
则n=
×
.
故∠O=
×
度;
(2)∵S扇形OAB=
l•OA,S扇形OA'B'=
l'•OA',
∴SABB′A′=S扇形OAB-S扇形OA'B'=
l•OA-
l'OA'=
l•(OA'+d)-
l'•OA'=
(l+l′)d.
 |
| AB |
| nπ•OA |
| 180 |
 |
| A′B′ |
| nπ•OA′ |
| 180 |
则OA=
| 180l |
| nπ |
| 180l′ |
| nπ |
∵OA-OA'=d,
则
| 180l |
| nπ |
| 180l′ |
| nπ |
则n=
| l-l′ |
| d |
| 180 |
| π |
故∠O=
| l-l′ |
| d |
| 180 |
| π |
(2)∵S扇形OAB=
| 1 |
| 2 |
| 1 |
| 2 |
∴SABB′A′=S扇形OAB-S扇形OA'B'=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了弧长公式以及扇形的面积公式,理解公式是关键.

练习册系列答案
相关题目
 直角三角形纸片的两直角边长分别为6,8,现将△ABC如右图折叠,使点A和点B重合,则折痕DE的长是( )
直角三角形纸片的两直角边长分别为6,8,现将△ABC如右图折叠,使点A和点B重合,则折痕DE的长是( )| A、3 | B、3.5 | C、3.75 | D、4 |

 如图,一张圆心角为45°的扇形纸板按如图方式剪得一个正方形,正方形的边长为1,则扇形纸板的面积是
如图,一张圆心角为45°的扇形纸板按如图方式剪得一个正方形,正方形的边长为1,则扇形纸板的面积是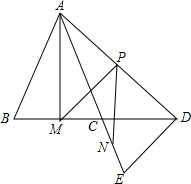 如图,已知AE与BD相交于点C,AB=AC,DE=DC,M、N、P分别是BC、CE、AD的中点.求证:
如图,已知AE与BD相交于点C,AB=AC,DE=DC,M、N、P分别是BC、CE、AD的中点.求证: