题目内容
14. 函数y=$\frac{4}{x}$和y=$\frac{1}{x}$在第一象限内的图象如图所示,点P是y=$\frac{4}{x}$的图象上一动点,作PC⊥x轴于点C,交y=$\frac{1}{x}$的图象于点A,作PD⊥y轴于点D,交y=$\frac{1}{x}$的图象于点B,给出如下结论:①△ODB与△OCA的面积相等;②PA与PB始终相等;③四边形PAOB的面积大小不会发生变化;④PA=3AC,其中正确的结论序号是( )
函数y=$\frac{4}{x}$和y=$\frac{1}{x}$在第一象限内的图象如图所示,点P是y=$\frac{4}{x}$的图象上一动点,作PC⊥x轴于点C,交y=$\frac{1}{x}$的图象于点A,作PD⊥y轴于点D,交y=$\frac{1}{x}$的图象于点B,给出如下结论:①△ODB与△OCA的面积相等;②PA与PB始终相等;③四边形PAOB的面积大小不会发生变化;④PA=3AC,其中正确的结论序号是( )| A. | ①②③ | B. | ②③④ | C. | ①③④ | D. | ①②④ |
分析 设点P的坐标为(m,$\frac{4}{m}$)(m>0),则A(m,$\frac{1}{m}$),C(m,0),B($\frac{m}{4}$,$\frac{4}{m}$),D(0,$\frac{4}{m}$).①根据反比例函数系数k的几何意义即可得出S△ODB=S△OCA,该结论正确;②由点的坐标可找出PA=$\frac{3}{m}$,PB=$\frac{3m}{4}$,由此可得出只有m=2是PA=PB,该结论不成;③利用分割图形法求图形面积结合反比例系数k的几何意义即可得知该结论成立;④结合点的坐标即可找出PA=$\frac{3}{m}$,AC=$\frac{1}{m}$,由此可得出该结论成立.综上即可得出正确的结论为①③④.
解答 解:设点P的坐标为(m,$\frac{4}{m}$)(m>0),则A(m,$\frac{1}{m}$),C(m,0),B($\frac{m}{4}$,$\frac{4}{m}$),D(0,$\frac{4}{m}$).
①S△ODB=$\frac{1}{2}$×1=$\frac{1}{2}$,S△OCA=$\frac{1}{2}$×1=$\frac{1}{2}$,
∴△ODB与△OCA的面积相等,①成立;
②PA=$\frac{4}{m}$-$\frac{1}{m}$=$\frac{3}{m}$,PB=m-$\frac{m}{4}$=$\frac{3m}{4}$,
令PA=PB,即$\frac{3}{m}$=$\frac{3m}{4}$,
解得:m=2.
∴当m=2时,PA=PB,②不正确;
③S四边形PAOB=S矩形OCPD-S△ODB-S△OCA=4-$\frac{1}{2}$-$\frac{1}{2}$=3.
∴四边形PAOB的面积大小不会发生变化,③正确;
④∵PA=$\frac{4}{m}$-$\frac{1}{m}$=$\frac{3}{m}$,AC=$\frac{1}{m}$-0=$\frac{1}{m}$,
∵$\frac{3}{m}$=3×$\frac{1}{m}$,
∴PA=3AC,④正确.
综上可知:正确的结论有①③④.
故选C.
点评 本题考查了反比例函数图象上点的坐标特征、反比例函数系数k的几何意义以及利用分割图形法求图形面积,解题的关键是找出各点坐标再结合反比例函数系数k的几何意义逐项分析各结论是否正确.本题属于中档题,难度不大,解决该题型题目时,根据反比例函数图象上点的坐标特征表示出各点的坐标是关键.

| A. | p=1,q=-12 | B. | p=-1,q=-12 | C. | p=7,q=12 | D. | p=7,q=-12 |
 如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,∠1=∠C.
如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,∠1=∠C. 如图,在矩形ABCD中,BC=10,AB=4,动点E从点B出发沿BC向终点C以每秒1个单位长度的速度运动,动点F沿折线BA-AD向终点D以每秒2个单位长度的速度运动,过点E作BF的平行线与过点F作BE的平行线相交于点G,若点E,F同时出发,当有一个点到达终点时,另一个点继续运动直至到达终点停止,四边形BEGF与矩形ABCD重叠部分的面积为S(平方单位),运动的时间为t(秒).
如图,在矩形ABCD中,BC=10,AB=4,动点E从点B出发沿BC向终点C以每秒1个单位长度的速度运动,动点F沿折线BA-AD向终点D以每秒2个单位长度的速度运动,过点E作BF的平行线与过点F作BE的平行线相交于点G,若点E,F同时出发,当有一个点到达终点时,另一个点继续运动直至到达终点停止,四边形BEGF与矩形ABCD重叠部分的面积为S(平方单位),运动的时间为t(秒).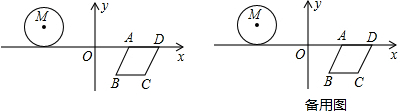
 如图,在假日游玩期间,小敏同学到光岳楼游玩.同时她想测量光岳楼AB的高度,已知在C点处,小敏利用测角仪测得∠BAC=30°,她向前走40米到达D点,测得∠BDA=60°,求光岳楼AB的高度(注:点B、D、C在同一直线上,测角仪的高度忽略不计,结果保留根号)
如图,在假日游玩期间,小敏同学到光岳楼游玩.同时她想测量光岳楼AB的高度,已知在C点处,小敏利用测角仪测得∠BAC=30°,她向前走40米到达D点,测得∠BDA=60°,求光岳楼AB的高度(注:点B、D、C在同一直线上,测角仪的高度忽略不计,结果保留根号)