题目内容
6.(1)计算:$\frac{m+n}{m-n}+\frac{2m}{n-m}$;(2)先化简,再求值:($\frac{x^2+4}{x}$-4)÷$\frac{x^2-4}{x^2+2x}$,其中x=1.
分析 (1)先通分,再把分子相加减即可;
(2)先算括号里面的,再算除法即可.
解答 解:(1)原式=$\frac{m+n}{m-n}-\frac{2m}{m-n}$
=$\frac{m+n-2m}{m-n}$=$\frac{n-m}{m-n}$
=-1;
(2)原式=$\frac{{x}^{2}+4-4x}{x}$•$\frac{x(x+2)}{(x+2)(x-2)}$
=$\frac{(x-2)^{2}}{x}$•$\frac{x(x+2)}{(x+2)(x-2)}$
=x-2,
当x=1时,原式=1-2=-1.
点评 本题考查的是分式的混合运算,熟知分式的混合运算,要注意运算顺序,式与数有相同的混合运算顺序;先乘方,再乘除,然后加减,有括号的先算括号里面的是解答此题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
16.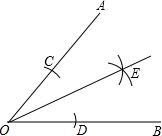 观察图中尺规作图痕迹,下列说法错误的是( )
观察图中尺规作图痕迹,下列说法错误的是( )
 观察图中尺规作图痕迹,下列说法错误的是( )
观察图中尺规作图痕迹,下列说法错误的是( )| A. | OE是∠AOB的平分线 | B. | OC=OD | ||
| C. | 点C、D到OE的距离不相等 | D. | ∠AOE=∠BOE |
16.计算:($\frac{1}{2}$)-1-(π-1)0,结果正确的是( )
| A. | 2 | B. | 1 | C. | -$\frac{1}{2}$ | D. | -$\frac{3}{2}$ |
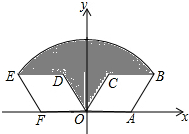 如图,菱形OABC的顶点A的坐标为(2,0),∠COA=60°,将菱形OABC绕坐标原点O逆时针旋转120°得到菱形ODEF,则图中阴影部分的面积为4π-2$\sqrt{3}$.
如图,菱形OABC的顶点A的坐标为(2,0),∠COA=60°,将菱形OABC绕坐标原点O逆时针旋转120°得到菱形ODEF,则图中阴影部分的面积为4π-2$\sqrt{3}$. 函数y=$\frac{4}{x}$和y=$\frac{1}{x}$在第一象限内的图象如图所示,点P是y=$\frac{4}{x}$的图象上一动点,作PC⊥x轴于点C,交y=$\frac{1}{x}$的图象于点A,作PD⊥y轴于点D,交y=$\frac{1}{x}$的图象于点B,给出如下结论:①△ODB与△OCA的面积相等;②PA与PB始终相等;③四边形PAOB的面积大小不会发生变化;④PA=3AC,其中正确的结论序号是( )
函数y=$\frac{4}{x}$和y=$\frac{1}{x}$在第一象限内的图象如图所示,点P是y=$\frac{4}{x}$的图象上一动点,作PC⊥x轴于点C,交y=$\frac{1}{x}$的图象于点A,作PD⊥y轴于点D,交y=$\frac{1}{x}$的图象于点B,给出如下结论:①△ODB与△OCA的面积相等;②PA与PB始终相等;③四边形PAOB的面积大小不会发生变化;④PA=3AC,其中正确的结论序号是( )