题目内容
14.平面坐标系中,点A坐标为(2,1),连接OA把线段OA绕原点O逆时针旋转90°,那么OA扫过的面积是$\frac{5}{4}$π.分析 由勾股定理得到OA=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,然后根据扇形的面积公式即可得到结论.
解答 解:∵点A坐标为(2,1),
∴OA=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,
∴OA扫过的面积=$\frac{90•π×(\sqrt{5})^{2}}{360}$=$\frac{5}{4}$π,
故答案为:$\frac{5}{4}$π.
点评 本题考查了扇形的面积,旋转的性质,熟记扇形的面积公式是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.某数学老师为了了解学生在数学学习中常见错误的纠正情况,收集整理了学生在作业和考试中的常见错误,编制了10道选择题,每题3分,对他所教的初三(1)班(2)班进行了检测.如图表示从两班各随机抽取的10名学生的得分情况:
(1)利用图中提供的信息,补全下表:
(2)若把24分以上(含24分)记为”优秀”,两班各50名学生,请估计两班各有多少名学生成绩优秀;
(3)观察图中数据分布情况,请通过计算说明哪个班的学生纠错的得分情况更稳定.
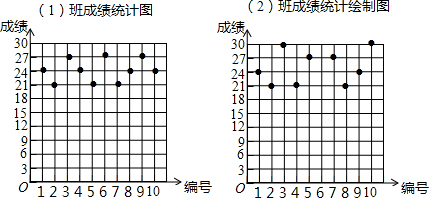
(1)利用图中提供的信息,补全下表:
| 班级 | 平均数(分) | 中位数(分) | 众数(分) |
| (1)班 | 24 | 24 | 24 |
| (2)班 | 24 | 24 | 21 |
(3)观察图中数据分布情况,请通过计算说明哪个班的学生纠错的得分情况更稳定.

2.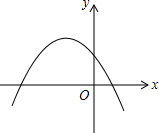 已知抛物线y=ax2+bx+c的图象如图所示,则直线y=ax-b一定不经过( )
已知抛物线y=ax2+bx+c的图象如图所示,则直线y=ax-b一定不经过( )
 已知抛物线y=ax2+bx+c的图象如图所示,则直线y=ax-b一定不经过( )
已知抛物线y=ax2+bx+c的图象如图所示,则直线y=ax-b一定不经过( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 如图,在菱形ABCD中,∠BCD=108°,CD的垂直平分线交对角线AC于点F,E为垂足,连结BF,则∠ABF等于18°.
如图,在菱形ABCD中,∠BCD=108°,CD的垂直平分线交对角线AC于点F,E为垂足,连结BF,则∠ABF等于18°.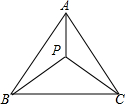 如图,等边△ABC中,AB=4,P是△ABC中的任意一点,连接PA、PB、PC,则PA+PB+PC的最小值为4$\sqrt{3}$.
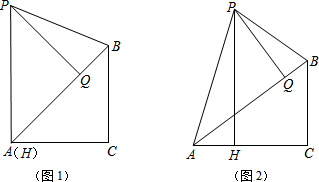
如图,等边△ABC中,AB=4,P是△ABC中的任意一点,连接PA、PB、PC,则PA+PB+PC的最小值为4$\sqrt{3}$.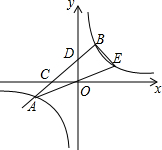 如图,直线AB与双曲线交于点A,B,与x轴,y轴分别交于点C,D,与x轴的夹角α满足tanα=$\frac{3}{4}$,且OD=6,CD:CB=1:2.
如图,直线AB与双曲线交于点A,B,与x轴,y轴分别交于点C,D,与x轴的夹角α满足tanα=$\frac{3}{4}$,且OD=6,CD:CB=1:2.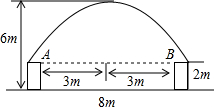 某一隧道内设双行线公路,其截面由一长方形和一抛物线构成,如图所示,为保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方向上高度之差至少要有0.5m,若行车道总宽度AB为6m,请计算车辆经过隧道时的限制高度是多少米?(精确到0.1m)
某一隧道内设双行线公路,其截面由一长方形和一抛物线构成,如图所示,为保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方向上高度之差至少要有0.5m,若行车道总宽度AB为6m,请计算车辆经过隧道时的限制高度是多少米?(精确到0.1m)