题目内容
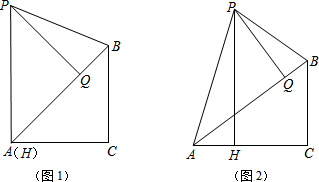
5.在Rt△ABC中,∠C=90°,AC=1,将△ABC绕点A逆时针旋转,得到△APQ,点C的对应点Q落在AB边上.连接BP,过点P作PH垂直于射线CA,垂足为H.(1)如图1,若点H与点A重合,求∠BPQ的度数;
(2)如图2,若点H在CA边上(不与点A重合),BC=x,请用含x的代数式表示AH;
(3)若∠APB=∠PAH,求AB的长.
分析 (1)由旋转得到△ABC≌APQ,再判断出△APQ为等腰直角三角形,最后进行计算即可;
(2)先求出AB=$\sqrt{{x}^{2}+1}$,再用△ABC∽△PMQ,表示出AM,最后△AMH∽△ABC求出AH,
(3)先判断出△PAB和△ABD是等腰三角形,用△APB∽△DPA得到比例式列出方程,求解即可.
解答 解:(1)由旋转得,△ABC≌APQ,
∴∠PAQ=∠BAC,AP=AB,AQ=AC,PQ=BC,PQ⊥AB,
∵PH⊥AC,
∴∠PAC=90°,
∴∠PAQ=∠BAC=45°,
∴△APQ为等腰直角三角形,
∴∠APQ=45°,
∵AP=AB,
∴∠APB=∠ABP=67.5°,
∴∠BPQ=∠APB-∠APQ=22.5°,
(2)由旋转得,AQ=AC=1,PQ=BC=x,
∴AB=$\sqrt{{x}^{2}+1}$,
设PH交AB于M,
∴△ABC∽△PMQ,
∴$\frac{MQ}{BC}=\frac{PQ}{AC}$,
∴$\frac{MQ}{x}=\frac{x}{1}$,
∴MQ=x2,
∴AM=1-x2,
∵△AMH∽△ABC,
∴$\frac{AM}{AB}=\frac{AH}{AC}$,
∴$\frac{1-{x}^{2}}{\sqrt{{x}^{2}+1}}=\frac{AH}{1}$,
∴AH=$\frac{1-{x}^{2}}{\sqrt{{x}^{2}+1}}$,
(3)①当点H在线段AC上时,如图1,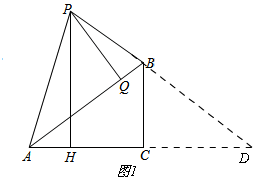
延长PD交AC延长线于D,
∴∠PAB=∠BAC=$\frac{1}{2}$∠PAH,∠APB=∠ABP,
∵∠PAH=∠APB,
∴∠APB=∠ABP=2∠PAB,
∴∠PAB=∠BAC=36°,∠APB=∠PAH=72°,
∴∠D=∠BAC=36°,
∴△PAB和△ABD是等腰三角形,
∴AP=AB=BD,AD=PD,
∵BC⊥AC,
∴PD=AD=2AC=2,
设AB=x,
∵△APB∽△DPA,
∴$\frac{PB}{AP}=\frac{AP}{PD}$,
∴$\frac{PB}{x}=\frac{x}{2}$,
∴PB=$\frac{1}{2}$x2,
∵BD=PD-PB,
∴x=2-$\frac{1}{2}$x2,
∴x=-1+$\sqrt{5}$或x=-1-$\sqrt{5}$(舍),
∴AB=-1+$\sqrt{5}$.
②当点H在射线CA上时,如图2,
∵∠APB=∠PAH,
∴PB∥HC,
∵∠H=∠C=90°,PA=AB,
∴△PAH≌△BAC,
∴AH=AC=1,
∵PA=BA,
∴∠APB=∠ABP=∠PAD,
∴△ADP∽△PAB,
设AB=x,
∴$\frac{PB}{AP}=\frac{AP}{PD}$,
∴$\frac{2}{x}=\frac{x}{PD}$,
∴PD=$\frac{1}{2}$x2,
∵BD=PB-PD,
∴x=2-$\frac{1}{2}$x2,
∴x=-1+$\sqrt{5}$或x=-1-$\sqrt{5}$(舍),
∴AB=-1+$\sqrt{5}$
即:AB的长为-1+$\sqrt{5}$.
点评 此题是几何变换综合题,主要考查了等腰三角形的判定和性质,相似三角形的性质和判定,勾股定理,解本题的关键是用相似得到的比例式表示线段.

 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
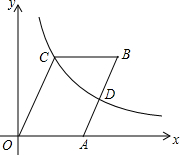 如图,?OABC的顶点B、C在第一象限,点A的坐标为(3,0),D为边AB的中点,反比例函数y=$\frac{k}{x}$(k>0)的图象经过点C、D两点,若∠COA=60°,则k的值为4$\sqrt{3}$.
如图,?OABC的顶点B、C在第一象限,点A的坐标为(3,0),D为边AB的中点,反比例函数y=$\frac{k}{x}$(k>0)的图象经过点C、D两点,若∠COA=60°,则k的值为4$\sqrt{3}$. 研究几何图形,我们往往先给出这类图形的定义,再研究它的性质和判定方法.我们给出如下定义:如图,四边形ABCD中,AB=AD,CB=CD像这样两组邻边分别相等的四边形叫做“筝形”;
研究几何图形,我们往往先给出这类图形的定义,再研究它的性质和判定方法.我们给出如下定义:如图,四边形ABCD中,AB=AD,CB=CD像这样两组邻边分别相等的四边形叫做“筝形”;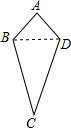
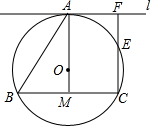 过⊙0上一点A作⊙0的切线l∥弦BC,过C作直线m⊥l于F,交⊙0于点E,
过⊙0上一点A作⊙0的切线l∥弦BC,过C作直线m⊥l于F,交⊙0于点E,