题目内容
4.某数学老师为了了解学生在数学学习中常见错误的纠正情况,收集整理了学生在作业和考试中的常见错误,编制了10道选择题,每题3分,对他所教的初三(1)班(2)班进行了检测.如图表示从两班各随机抽取的10名学生的得分情况:(1)利用图中提供的信息,补全下表:
| 班级 | 平均数(分) | 中位数(分) | 众数(分) |
| (1)班 | 24 | 24 | 24 |
| (2)班 | 24 | 24 | 21 |
(3)观察图中数据分布情况,请通过计算说明哪个班的学生纠错的得分情况更稳定.
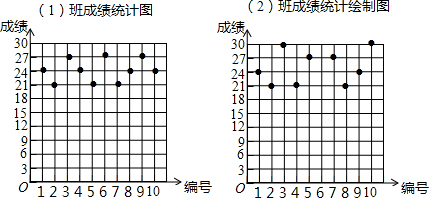
分析 (1)将图(1)中数据相加再除以10,即可到样本平均数;找到图(2)中出现次数最多的数和处于中间位置的数,即为众数和中位数;
(2)找到样本中24分和24分人数所占的百分数,用样本平均数估计总体平均数;
(3)计算出两个班的方差,方差越小越稳定.
解答 解:24×10-(24+21+30+21+27+27+21+24+30)
=240-225
=15
(1)(1)班平均分:$\frac{1}{10}$(24+21+27+24+21+27+21+24+27+24)=24;
有4名学生24分,最多,故众数为24分;
处于中间位置的数为24和24,故中位数为24,出现次数最多的数为24,故众数为24.
| 班级 | 平均数(分) | 中位数(分) | 众数(分) |
| (1)班 | 24 | 24 | |
| (2)班 | 24 |
三(1)班成绩优秀的学生有50×$\frac{7}{10}$=35名;
(2)班优秀率为$\frac{6}{10}$,
三(2)班成绩优秀的学生有50×$\frac{6}{10}$=30名;
(3)S12=$\frac{1}{10}$[(21-24)2×3+(24-24)2×4+(27-24)2×3]
=$\frac{1}{10}$×(27+27)
=5.4;
S22=$\frac{1}{10}$[(21-24)2×3+(24-24)2×2+(27-24)2×2+(30-24)2×2+(15-24)2]
=$\frac{1}{10}$×198
=19.8;
S12<S22,初三(1)班成绩比较整齐.
点评 本题考查了方差、算术平均数、众数和中位数,熟悉各统计量的意义及计算方法是解题的关键.

练习册系列答案
相关题目
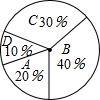 某校260名学生参加植树活动,要求每人植4-7棵,活动结束后随机调查了部分学生每人的植树量,并分为四种类型,A:4棵;B:5棵;C:6棵;D:7棵.并结合调查数据作出如图所示的扇形统计图,根据统计图提供的信息,可估算出该校植树量达到6棵的学生有( )
某校260名学生参加植树活动,要求每人植4-7棵,活动结束后随机调查了部分学生每人的植树量,并分为四种类型,A:4棵;B:5棵;C:6棵;D:7棵.并结合调查数据作出如图所示的扇形统计图,根据统计图提供的信息,可估算出该校植树量达到6棵的学生有( ) 如图,直角梯形ABCD中,∠B=90°,AD∥BC,BC=2AD,点E为边BC的中点.
如图,直角梯形ABCD中,∠B=90°,AD∥BC,BC=2AD,点E为边BC的中点.
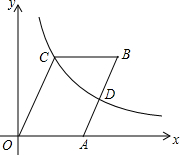 如图,?OABC的顶点B、C在第一象限,点A的坐标为(3,0),D为边AB的中点,反比例函数y=$\frac{k}{x}$(k>0)的图象经过点C、D两点,若∠COA=60°,则k的值为4$\sqrt{3}$.
如图,?OABC的顶点B、C在第一象限,点A的坐标为(3,0),D为边AB的中点,反比例函数y=$\frac{k}{x}$(k>0)的图象经过点C、D两点,若∠COA=60°,则k的值为4$\sqrt{3}$.