题目内容
9. 如图,在菱形ABCD中,∠BCD=108°,CD的垂直平分线交对角线AC于点F,E为垂足,连结BF,则∠ABF等于18°.
如图,在菱形ABCD中,∠BCD=108°,CD的垂直平分线交对角线AC于点F,E为垂足,连结BF,则∠ABF等于18°.
分析 欲求∠ABF只要求出∠ABC、∠CBF,∠ABC,利用菱形的性质:邻角互补解决,∠CBF利用全等三角形的性质解决.
解答 解:连接DF.
∵四边形ABCD为菱形,∠BCD=108°,
∴∠DCA=∠BCA=54°,∠DCB+∠CBA=180°,
∴∠CBA=72°,
∵EF垂直平分CD,
∴FC=FD,
∴∠CDF=∠DCF=54°,
在△FCD和△FCB中,
$\left\{\begin{array}{l}{CF=CF}\\{∠FCD=∠FCB}\\{CD=CB}\end{array}\right.$,
∴△FCD≌△FCB,
∴∠CBF=∠CDF=54°,
∴∠ABF=∠ABC-∠CBF=72°-54°=18°.
故答案为18°.
点评 本题考查菱形的性质、线段垂直平分线的性质等知识,解题的关键是灵活运用全等三角形的性质,出现垂直平分线要想到垂直平分线的性质,利用这个性质添加辅助线,属于中考常考题型.

练习册系列答案
相关题目
1.表是校女子排球队队员的年龄分布.
求校女子排球队队员的平均年龄(结果取整数,可以使用计算器)
| 年龄 | 13 | 14 | 15 | 16 |
| 频数 | 1 | 4 | 5 | 2 |
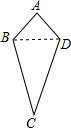
 研究几何图形,我们往往先给出这类图形的定义,再研究它的性质和判定方法.我们给出如下定义:如图,四边形ABCD中,AB=AD,CB=CD像这样两组邻边分别相等的四边形叫做“筝形”;
研究几何图形,我们往往先给出这类图形的定义,再研究它的性质和判定方法.我们给出如下定义:如图,四边形ABCD中,AB=AD,CB=CD像这样两组邻边分别相等的四边形叫做“筝形”;