题目内容
1.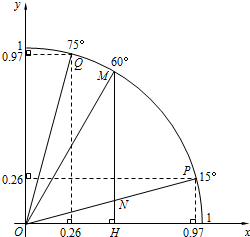 如图,点P、M、Q在半径为1的⊙O上,根据已学知识和图中数据(0.97、0.26为近似数),解答下列问题:
如图,点P、M、Q在半径为1的⊙O上,根据已学知识和图中数据(0.97、0.26为近似数),解答下列问题:(1)sin60°=$\frac{\sqrt{3}}{2}$;cos75°=0.26;
(2)若MH⊥x轴,垂足为H,MH交OP于点N,求MN的长.(结果精确到0.01,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
分析 (1)根据图形中的数据可以解答本题;
(2)要求MN的长,只要求出MH的长和NH的长,即可求得MN的长,根据题意可以求得MH和NH的长,本题得以解决.
解答 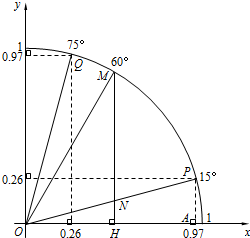 解:(1)由图可知,
解:(1)由图可知,
sin60°=$\frac{\sqrt{3}}{2}$,cos75°=$\frac{0.26}{1}$=0.26,
故答案为:$\frac{\sqrt{3}}{2}$;0.26;
(2)在Rt△MHO中,sin∠MOH=$\frac{MH}{MO}$,
即MH=MO•sin∠MOH=1×$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{2}$.
∴OH=$\sqrt{O{M}^{2}-M{H}^{2}}=\sqrt{{1}^{2}-(\frac{\sqrt{3}}{2})^{2}}=\frac{1}{2}$,
设PA⊥x轴,垂足为A,如右图所示,
∵∠NHO=∠PAO=90°,
∴NH∥PA,
∴△ONH∽△OPA,
∴$\frac{NH}{PA}$=$\frac{OH}{OA}$,即$\frac{NH}{0.26}$=$\frac{\frac{1}{2}}{0.97}$,
∴NH≈0.134.
∴MN=MH-MN=$\frac{\sqrt{3}}{2}-0.134$≈0.73.
点评 本题考查解直角三角形、相似三角形的性质和判定,解题的关键是明确题意,找出所求问题需要的条件.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.某校九年级共有450名学生,为了了解该年级学生的数学解题能力情况,该校数学兴趣小组随机抽取了90人进行调查分析,并将抽取的学生的数学解题成绩进行分组,绘制如下频数分布表和成绩分布扇形统计图(图1):
该校90名学生数学解题成绩频数分布表
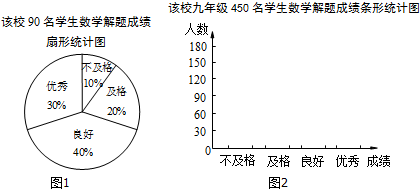
(1)根据抽样调查的结果,将估计出该校九年级450名学生数学解题成绩情况在图2中绘制成条形统计图:
(2)请你结合上述统计的结果,提出一条合理化建议.
该校90名学生数学解题成绩频数分布表
| 成绩 | 划记 | 频数 |
| 不及格 | 正 | 9 |
| 及格 | 正正正 | 18 |
| 良好 | 正正正正正正一 | 36 |
| 优秀 | 正正正正正 | 27 |
| 合计 | 90 |

(1)根据抽样调查的结果,将估计出该校九年级450名学生数学解题成绩情况在图2中绘制成条形统计图:
(2)请你结合上述统计的结果,提出一条合理化建议.
16.由4名同学每人写一个实系数一元二次方程,所得的四个方程中恰有两个无实数根的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{5}$ | D. | $\frac{3}{8}$ |
 如图,已知CD⊥AB,垂足为D,EF⊥AB,垂足为F.
如图,已知CD⊥AB,垂足为D,EF⊥AB,垂足为F. 如图,抛物线y=ax2+bx+2与x轴交于点A(-1,0),B(4,0)两点,与y轴交于点C,与过点C且平行x轴的直线交于另一点D.
如图,抛物线y=ax2+bx+2与x轴交于点A(-1,0),B(4,0)两点,与y轴交于点C,与过点C且平行x轴的直线交于另一点D.