题目内容
12.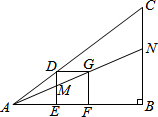 如图的△ABC中有一正方形DEFG,其中D在AC上,E、F在AB上,直线AG分别交DE、BC于M、N两点.若∠B=90°,AB=4,BC=3,EF=1,则BN的长度为何?( )
如图的△ABC中有一正方形DEFG,其中D在AC上,E、F在AB上,直线AG分别交DE、BC于M、N两点.若∠B=90°,AB=4,BC=3,EF=1,则BN的长度为何?( )| A. | $\frac{4}{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{8}{5}$ | D. | $\frac{12}{7}$ |
分析 由DE∥BC可得$\frac{AE}{AB}=\frac{DE}{BC}$求出AE的长,由GF∥BN可得$\frac{AE+EF}{AB}=\frac{GF}{BN}$,将AE的长代入可求得BN.
解答 解:∵四边形DEFG是正方形,
∴DE∥BC,GF∥BN,且DE=GF=EF=1,
∴△ADE∽△ACB,△AGF∽△ANB,
∴$\frac{AE}{AB}=\frac{DE}{BC}$ ①,$\frac{AE+EF}{AB}=\frac{GF}{BN}$ ②,
由①可得,$\frac{AE}{4}=\frac{1}{3}$,解得:AE=$\frac{4}{3}$,
将AE=$\frac{4}{3}$代入②,得:$\frac{\frac{4}{3}+1}{4}=\frac{1}{BN}$,
解得:BN=$\frac{12}{7}$,
故选:D.
点评 本题主要考查正方形的性质及相似三角形的判定与性质,根据相似三角形的性质得出AE的长是解题的关键.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
2.下列计算正确的是( )
| A. | a3+a3=a6 | B. | 3a-a=3 | C. | (a3)2=a5 | D. | a•a2=a3 |
7.判断2$\sqrt{11}$-1之值介于下列哪两个整数之间?( )
| A. | 3,4 | B. | 4,5 | C. | 5,6 | D. | 6,7 |
17. 如图数轴的A、B、C三点所表示的数分别为a、b、c.若|a-b|=3,|b-c|=5,且原点O与A、B的距离分别为4、1,则关于O的位置,下列叙述何者正确?( )
如图数轴的A、B、C三点所表示的数分别为a、b、c.若|a-b|=3,|b-c|=5,且原点O与A、B的距离分别为4、1,则关于O的位置,下列叙述何者正确?( )
 如图数轴的A、B、C三点所表示的数分别为a、b、c.若|a-b|=3,|b-c|=5,且原点O与A、B的距离分别为4、1,则关于O的位置,下列叙述何者正确?( )
如图数轴的A、B、C三点所表示的数分别为a、b、c.若|a-b|=3,|b-c|=5,且原点O与A、B的距离分别为4、1,则关于O的位置,下列叙述何者正确?( )| A. | 在A的左边 | B. | 介于A、B之间 | C. | 介于B、C之间 | D. | 在C的右边 |
4.若一正方形的面积为20平方公分,周长为x公分,则x的值介于下列哪两个整数之间?( )
| A. | 16,17 | B. | 17,18 | C. | 18,19 | D. | 19,20 |
 如图,OA,OB是⊙O的半径,点C在⊙O上,连接AC,BC,若∠AOB=120°,则∠ACB=60度.
如图,OA,OB是⊙O的半径,点C在⊙O上,连接AC,BC,若∠AOB=120°,则∠ACB=60度.