题目内容
1.已知$\frac{x}{y+z}$=$\frac{y}{x+z}$=$\frac{z}{x+y}$,求$\frac{x+y}{z}$的值.分析 根据等比性质,可得$\frac{z}{x+y}$,根据反比性质,可得答案.
解答 解:由等比性质,得
$\frac{z}{x+y}$=$\frac{x+y+z}{y+z+x+z+x+y}$=$\frac{1}{2}$.
由反比性质,得
$\frac{x+y}{2}$=$\frac{2}{1}$=2.
点评 本题考查了比例的性质,利用了等比性质:$\frac{a}{b}$=$\frac{c}{d}$⇒$\frac{a}{b}$=$\frac{a+c}{b+d}$,反比性质:$\frac{a}{b}$=$\frac{c}{d}$⇒$\frac{b}{a}$=$\frac{d}{c}$.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
12.把8000用科学记数法表示是( )
| A. | 80×102 | B. | 8×103 | C. | 0.8×104 | D. | 8×104 |
6.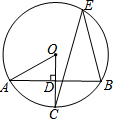 如图,A,B,E为⊙O上的点,⊙O的半径OC⊥AB于点D,若∠CEB=30°,OD=1,则AB的长为( )
如图,A,B,E为⊙O上的点,⊙O的半径OC⊥AB于点D,若∠CEB=30°,OD=1,则AB的长为( )
 如图,A,B,E为⊙O上的点,⊙O的半径OC⊥AB于点D,若∠CEB=30°,OD=1,则AB的长为( )
如图,A,B,E为⊙O上的点,⊙O的半径OC⊥AB于点D,若∠CEB=30°,OD=1,则AB的长为( )| A. | $\sqrt{3}$ | B. | 4 | C. | 2$\sqrt{3}$ | D. | 6 |
10.在所给的π,0,-1,$\sqrt{2}$这四个数中,最小的数是( )
| A. | π | B. | 0 | C. | -1 | D. | $\sqrt{2}$ |
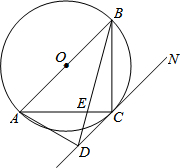 如图,AB是⊙O的直径,C是弧AB的中点,D是⊙O的切线CN上一点,BD交AC于点E,且BA=BD.
如图,AB是⊙O的直径,C是弧AB的中点,D是⊙O的切线CN上一点,BD交AC于点E,且BA=BD.