题目内容
15. 完成下面的证明,在括号内加注理由.
完成下面的证明,在括号内加注理由.如图,AB∥CD,∠B+∠D=180°.
求证:BC∥DE.
证明:∵AB∥CD(已知),
∴∠B=∠C(两直线平行,内错角相等),
∵∠B+∠D=180°,
∴∠C+∠D=180°(等量代换)
∴BC∥DE(同旁内角互补,两直线平行)
分析 首先根据平行线的性质可得∠B=∠C,再由∠B+∠D=180°,可得∠C+∠D=180°,根据同旁内角互补两直线平行可得CB∥DE.
解答 证明:∵AB∥CD(已知),
∴∠B=∠C(两直线平行,内错角相等),
∵∠B+∠D=180°,
∴∠C+∠D=180°(等量代换)
∴BC∥DE(同旁内角互补,两直线平行),
故答案为:已知,两直线平行,内错角相等,∠C,等量代换,同旁内角互补,两直线平行.
点评 此题主要考查了平行线的判定与性质,关键是掌握平行线的判定是由角的数量关系判断两直线的位置关系.平行线的性质是由平行关系来寻找角的数量关系.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
6.解方程组$\left\{\begin{array}{l}{26x+29y=3,(1)}\\{29x+26y=-3,(2)}\end{array}\right.$,下列四种方法中,最简便的是( )
| A. | 代入消元法 | B. | (1)×29-(2)×26,先消去x | ||
| C. | (1)×26-(2)×29,先消去y | D. | (1)+(2),两方程相加 |
10.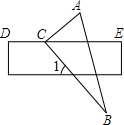 将一块含60°角的三角板ACB和直尺如图放置,使三角板的直角顶点C落在直尺的DE边上,若CE平分∠ACB,则∠1的度数是( )
将一块含60°角的三角板ACB和直尺如图放置,使三角板的直角顶点C落在直尺的DE边上,若CE平分∠ACB,则∠1的度数是( )
 将一块含60°角的三角板ACB和直尺如图放置,使三角板的直角顶点C落在直尺的DE边上,若CE平分∠ACB,则∠1的度数是( )
将一块含60°角的三角板ACB和直尺如图放置,使三角板的直角顶点C落在直尺的DE边上,若CE平分∠ACB,则∠1的度数是( )| A. | 135° | B. | 60° | C. | 50° | D. | 45° |
4.若一个多边形的外角和与它的内角和相等,则这个多边形是( )
| A. | 三角形 | B. | 五边形 | C. | 四边形 | D. | 六边形 |
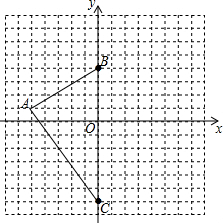 已知△ABC的顶点在坐标系中的坐标分别为:A(-5,1)、B(0,4)、C(0,-6).
已知△ABC的顶点在坐标系中的坐标分别为:A(-5,1)、B(0,4)、C(0,-6). 如图,在△ABC中,AB=5厘米,BC=3厘米,BM为中线,则△ABM与△BCM的周长之差是2厘米.
如图,在△ABC中,AB=5厘米,BC=3厘米,BM为中线,则△ABM与△BCM的周长之差是2厘米.