题目内容
5.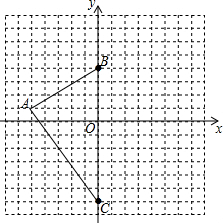 已知△ABC的顶点在坐标系中的坐标分别为:A(-5,1)、B(0,4)、C(0,-6).
已知△ABC的顶点在坐标系中的坐标分别为:A(-5,1)、B(0,4)、C(0,-6).(1)将△ABC向右平移3个单位,再向上平移1个单位后的△A1B1C1.请在坐标系中画出△A1B1C1,并写出点A1、B1、C1的坐标分别为(-2,2),(3,5),(3,-5).
(2)若A1C1,A1B1与y轴分别交于D、E两点,则DE=4.
分析 (1)根据图形平移的性质画出图形,并写出点A1、B1、C1的坐标即可;
(2)利用待定系数法求出直线A1C1,A1B1与的解析式,故可得出D、E两点的坐标,进而可得出DE的长.
解答  解:(1)如图所示,由图可知A1(-2,2),B1(3,5),C1(3,-5).
解:(1)如图所示,由图可知A1(-2,2),B1(3,5),C1(3,-5).
故答案为:(-2,2),(3,5),(3,-5);
(2)设直线A1C1的解析式为y=kx+b(k≠0),
∵A1(-2,2),C1(3,-5).
∴$\left\{\begin{array}{l}-2k+b=2\\ 3k+b=-5\end{array}\right.$,解得$\left\{\begin{array}{l}k=-\frac{7}{5}\\ b=-\frac{4}{5}\end{array}\right.$,
∴直线A1C1的解析式为y=-$\frac{7}{5}$x-$\frac{4}{5}$,
∴D(0,-$\frac{4}{5}$).
设直线A1B1的解析式为y=ax+c(k≠0),
∵A1(-2,2),B1(3,5),
∴$\left\{\begin{array}{l}-2a+c=2\\ 3a+c=5\end{array}\right.$,解得$\left\{\begin{array}{l}a=\frac{3}{5}\\ c=\frac{16}{5}\end{array}\right.$,
∴直线A1B1的解析式为y=$\frac{3}{5}$x+$\frac{16}{5}$,
∴E(0,$\frac{16}{5}$),
∴DE=$\frac{16}{5}$+$\frac{4}{5}$=4.
故答案为:4.
点评 本题考查的是作图-平移变换,熟知图形平移不变性的性质是解答此题的关键.

练习册系列答案
相关题目
20.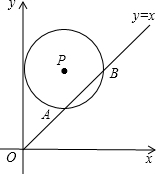 如图,在平面直角坐标系中,与y轴相切的⊙P的圆心是(2,a)且(a>2),
如图,在平面直角坐标系中,与y轴相切的⊙P的圆心是(2,a)且(a>2),
函数y=x的图象被⊙P截得的弦AB的长为2$\sqrt{3}$,则a的值是( )
 如图,在平面直角坐标系中,与y轴相切的⊙P的圆心是(2,a)且(a>2),
如图,在平面直角坐标系中,与y轴相切的⊙P的圆心是(2,a)且(a>2),函数y=x的图象被⊙P截得的弦AB的长为2$\sqrt{3}$,则a的值是( )
| A. | 2$\sqrt{3}$ | B. | 2+$\sqrt{3}$ | C. | 2+$\sqrt{2}$ | D. | 2$\sqrt{2}$ |
17.下列化简或计算正确的是( )
| A. | $\sqrt{(-\sqrt{3})^{2}}$=-$\sqrt{3}$ | B. | $\sqrt{1\frac{1}{49}}$=1+$\frac{1}{7}$=$\frac{8}{7}$ | C. | ($\sqrt{6}-\sqrt{3}$)2=9-2$\sqrt{3}$ | D. | $\sqrt{24}$÷(-$\frac{1}{2}$$\sqrt{6}$)=-4 |
14.下列说法正确的是( )
| A. | 两个形状和大小相同的图形可看作其中一个是另一个经过平移得到的 | |
| B. | 边长相等的两个正方形一定可以通过平移得到 | |
| C. | 周长和面积均相等的两个图形一定由平移得到 | |
| D. | 由平移得到的两个图形的对应点连线相互平行或在同一条直线上 |
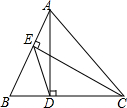 如图,已知在△ABC中,AD⊥BC,垂足为D,CE⊥AB,垂足为E,求证:△DBE∽△ABC.
如图,已知在△ABC中,AD⊥BC,垂足为D,CE⊥AB,垂足为E,求证:△DBE∽△ABC. 完成下面的证明,在括号内加注理由.
完成下面的证明,在括号内加注理由.