题目内容
20.若方程组$\left\{\begin{array}{l}{x+y=2k①}\\{x-y=4②}\end{array}\right.$的解满足$\left\{\begin{array}{l}{x>1}\\{y<1}\end{array}\right.$,求k的整数值.分析 把k看做已知数表示出方程组的解,代入已知不等式组中求出k的范围,即可确定出整数解.
解答 解:①+②得:2x=2k+4,即x=k+2,
①-②得:2y=2k-4,即y=k-2,
由题意得:$\left\{\begin{array}{l}{k+2>1}\\{k-2<1}\end{array}\right.$,
解得:-1<k<3,
则k的整数值为0,1,2.
点评 此题考查了二元一次方程组的解,方程组的解即为能使方程组中两方程都成立的未知数的值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.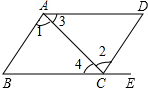 如图,给出下列条件:①∠1=∠2;②∠3=∠4;③∠B=∠DCE;④AD∥BC且∠B=∠D.其中,能推出AB∥DC的是( )
如图,给出下列条件:①∠1=∠2;②∠3=∠4;③∠B=∠DCE;④AD∥BC且∠B=∠D.其中,能推出AB∥DC的是( )
 如图,给出下列条件:①∠1=∠2;②∠3=∠4;③∠B=∠DCE;④AD∥BC且∠B=∠D.其中,能推出AB∥DC的是( )
如图,给出下列条件:①∠1=∠2;②∠3=∠4;③∠B=∠DCE;④AD∥BC且∠B=∠D.其中,能推出AB∥DC的是( )| A. | ①④ | B. | ②③ | C. | ①③ | D. | ①③④ |
10.下列命题是真命题的是( )
| A. | 两直线平行,同旁内角相等 | |
| B. | 三角形的一个外角大于任何一个内角 | |
| C. | 三角形三条边的垂直平分线相交于一点,且这一点到三边的距离相等 | |
| D. | 两角分别相等且其中一组等角的对边相等的两个三角形全等 |
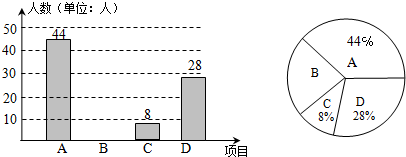
 完成下面的证明,在括号内加注理由.
完成下面的证明,在括号内加注理由.