题目内容
12.已知关于x的方程$\frac{2x+m}{x-2}=3$的解是正数,则m的取值范围为( )| A. | m<-6 | B. | m<-6且m≠-4 | C. | m>-6 | D. | m>-6且m≠-4 |
分析 先求出方程的解,再根据解为正数列出不等式,求出m的取值范围即可.
解答 解:去分母得,2x+m=3x-6,
移项合并得,x=m+6,
∵x>0,
∴m+6>0,
∴m>-6,
∵x-2≠0,
∴x≠2,
∴m+6≠2,
∴m≠-4,
∴m的取值范围为m>-6且m≠-4,
故选D.
点评 本题考查了分式方程的解,掌握解分式方程的步骤,注意验根是解题的关键.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
2.下列说法正确的是( )
| A. | 正数和负数统称为有理数 | B. | 负数的绝对值等于它的相反数 | ||
| C. | 两个负数中,绝对值大的数较大 | D. | 任何有理数都有倒数 |
3.在正方形、矩形、菱形、平行四边形、一般四边形中,两条对角线一定相等的四边形个数为( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
7.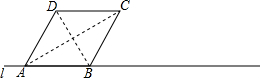 如图,菱形ABCD放置在直线l上(AB与直线l重合),AB=4,∠DAB=60°,将菱形ABCD沿直线l向右无滑动地在直线l上滚动,从点A离开出发点到点A第一次落在直线l上为止,点A运动经过的路径的长度为( )
如图,菱形ABCD放置在直线l上(AB与直线l重合),AB=4,∠DAB=60°,将菱形ABCD沿直线l向右无滑动地在直线l上滚动,从点A离开出发点到点A第一次落在直线l上为止,点A运动经过的路径的长度为( )
 如图,菱形ABCD放置在直线l上(AB与直线l重合),AB=4,∠DAB=60°,将菱形ABCD沿直线l向右无滑动地在直线l上滚动,从点A离开出发点到点A第一次落在直线l上为止,点A运动经过的路径的长度为( )
如图,菱形ABCD放置在直线l上(AB与直线l重合),AB=4,∠DAB=60°,将菱形ABCD沿直线l向右无滑动地在直线l上滚动,从点A离开出发点到点A第一次落在直线l上为止,点A运动经过的路径的长度为( )| A. | $\frac{8π}{3}$$+\frac{8\sqrt{3}π}{3}$ | B. | $\frac{16π}{3}$ | C. | $\frac{4π}{3}$+$\frac{4\sqrt{3}π}{3}$ | D. | $\frac{16\sqrt{3}π}{3}$ |
17.若方程组$\left\{\begin{array}{l}{x+y=3m①}\\{x-y=7m②}\end{array}\right.$的解也是二元一次方程3x+5y=10的解,则m的值应为( )
| A. | -2 | B. | 1 | C. | $\frac{1}{2}$ | D. | 2 |
1.$\sqrt{16}$等于( )
| A. | -4 | B. | 4 | C. | ±4 | D. | 256 |
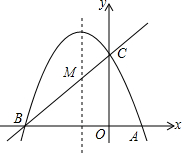 如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,且抛物线经过A(1,0),C(0,3)两点,抛物线与x轴的另一交点为B.
如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,且抛物线经过A(1,0),C(0,3)两点,抛物线与x轴的另一交点为B.
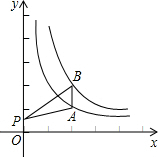 如图,点A在双曲线$y=\frac{2}{x}(x>0)$上,点B在双曲线$y=\frac{4}{x}(x>0)$上,且 AB∥y轴,点P是y轴上的任意一点,则△PAB的面积为( )
如图,点A在双曲线$y=\frac{2}{x}(x>0)$上,点B在双曲线$y=\frac{4}{x}(x>0)$上,且 AB∥y轴,点P是y轴上的任意一点,则△PAB的面积为( )