��Ŀ����
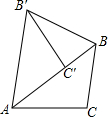
4����1�������龳����ͼ1����������ABCD�У�E��F��G��H�ֱ�ΪAB��BC��CD��DA���ϵĶ��㣬����EG��HF�ཻ�ڵ�O���ҡ�HOE=��ADC����̽����EG��FH��������ϵ����˵�����ɣ�
��2����չ���죺��ͼ2��������ABCD�У�E��F��G��H�ֱ�ΪAB��BC��CD��DA���ϵĶ��㣬����EG��HF�ཻ�ڵ�O���ҡ�HOE=��ADC����̽������1����EG��FH��������ϵ�������𣿲�˵�����ɣ�
��3����˼������������2���е�����ABCD��Ϊƽ���ı���ABCD����ͼ3����AB=a��AD=b�������������䣬��$\frac{EG}{FH}$=$\frac{b}{a}$�IJ�����ȷ����˵�����ɣ�
���� ��1����G��GM��AB��M����H��HN��BC��N���������ε����ʺ;��ε�������GM=HN���������ı��ε��ڽǺ�Ϊ360�㣬�ɵá�DHO+��DGE=360��-90��-90��=180�㣬�á�HFN=��GEM����AAS������֤�á�GME�ա�HNF������ȫ�������ε����ʿɵý��ۣ�
��2����G��GM��AB��M����H��HN��BC��N�������ε����ʿɵ�DC=AB=BC��AD��BC��DC��AB���������ε������ʽ��GM=HN����AAS��������֤�á�GME�ա�HNF����ȫ�������ε����ʿɵý��ۣ�
��3����G��GM��AB��M����H��HN��BC��N������ƽ���ı��ε����ʺ������ʽ�ɵ�$\frac{GM}{HN}=\frac{b}{a}$���á�GME�ס�HNF���������������ε����ʿɵò�����ȷ��
��� ��1���⣺EG=FH
�����ǣ���ͼ1����G��GM��AB��M����H��HN��BC��N��
���ı���ABCD�������Σ�
���D=��A=��B=��C=90�㣬
�֡�GM��AB��HN��BC
���ı���ADGM���ı���AHNB�Ǿ��Σ�
��HN=AB��AD=GM��
��HN=GM��
�ߡ�ADC=��HOE=90�㣬
���DHO+��DGE=360��-90��-90��=180�㣬
��AD��BC��DC��AB��
���NFH=��DHF����DGE+��GEM=180�㣬
���HFN=��GEM��
��HN��BC��GM��AB��
���GME=��HNF=90�㣬
�ڡ�GME�͡�HNF��$\left\{\begin{array}{l}{��GEM=��HFN}\\{��GME=��HNF}\\{GM=HN}\end{array}\right.$��
���GME�ա�HNF��AAS����
��EG=FH��
��2��EG=FH��
�����ǣ���ͼ2����G��GM��AB��M����H��HN��BC��N��
���ı���ABCD�����Σ�
��DC=AB=BC��AD��BC��DC��AB��
������ABCD�����S=AB��GM=BC��HN��
��GM=HN��
��GM��AB��HN��BC��
���GME=��HNF=90�㣬
�ߡ�ADC=��HOE��
���ADC+��HOG=��EOH+��HOG=180��
���DHO+��DGE=360��-180��=180�㣬
��AD��BC��DC��AB��
���NFH=��DHF����DGE+��GEM=180�㣬
���HFN=��GEM��
�ڡ�GME�͡�HNF��$\left\{\begin{array}{l}{��GEM=��HFN}\\{��GME=��HNF}\\{GM=HN}\end{array}\right.$��
���GME�ա�HNF��AAS����
��EG=FH��
��3����ȷ��
�����ǣ���ͼ3����G��GM��AB��M����H��HN��BC��N��
���ı���ABCD��ƽ���ı��Σ�
��AD��BC��DC��AB��
��ƽ���ı���ABCD�����S=AB��GM=BC��HN
��AB=a��AD=b��
��$\frac{GM}{HN}=\frac{b}{a}$��
��GM��AB��HN��BC��
���GME=��HNF=90�㣬
�ߡ�ADC=��HOE��
���ADC+��HOG=��EOH+��HOG=180�㣬
���DHO+��DGE=360��-180��=180�㣬
��AD��BC��DC��AB��
���NFH=��DHF����DGE+��GEM=180�㣬
���HFN=��GEM��
���GME�ס�HNF��
��$\frac{EG}{FH}=\frac{GM}{HN}=\frac{b}{a}$��
���� ������Ҫ�����������Σ����Σ�ƽ���ı��ε����ʣ�����ȫ�������κ������������ǽ�����Ĺؼ���

| A�� | 168Ԫ | B�� | 300Ԫ | C�� | 60Ԫ | D�� | 400Ԫ |
| A�� | m��-6 | B�� | m��-6��m��-4 | C�� | m��-6 | D�� | m��-6��m��-4 |
| A�� | �ĸ�����ֱ�� | B�� | ��������� | C�� | �Խ����ഹֱ | D�� | �Խ�����ƽ�� |
 ��ͼ��AB��CD���ǡ�O���ң���AB��CD������CDB=57�㣬���ACD�Ķ���Ϊ��������
��ͼ��AB��CD���ǡ�O���ң���AB��CD������CDB=57�㣬���ACD�Ķ���Ϊ��������| A�� | 33�� | B�� | 34�� | C�� | 43�� | D�� | 57�� |
 ��ͼ���ѡ�ABC�Ƶ�A��ʱ����ת42�㣬�õ���AB��C�䣬��C��ǡ�����ڱ�AB�ϣ�����BB�䣬���B��BC��Ĵ�СΪ69�㣮
��ͼ���ѡ�ABC�Ƶ�A��ʱ����ת42�㣬�õ���AB��C�䣬��C��ǡ�����ڱ�AB�ϣ�����BB�䣬���B��BC��Ĵ�СΪ69�㣮 ���������������ҹ��Ŵ����ݼ�Ϊ�ḻ����ѧ�������������������⣺������ί����ԫ�ڽǣ����ܰ˳ߣ�����ߣ��ʡ�����Ϊ���Σ�������˼Ϊ����������ǽ�Ǵ��ѷ��ף���ͼ����Ϊһ��Բ���ķ�֮һ�����ѵײ��Ļ���Ϊ8�ߣ��ѵĸ�Ϊ5�ߣ����ѵ�����Ͷѷŵ���Ϊ���٣�����֪1�������ԼΪ1.62�����ߣ�Բ����ԼΪ3��������ѷŵ���Լ�У�������
���������������ҹ��Ŵ����ݼ�Ϊ�ḻ����ѧ�������������������⣺������ί����ԫ�ڽǣ����ܰ˳ߣ�����ߣ��ʡ�����Ϊ���Σ�������˼Ϊ����������ǽ�Ǵ��ѷ��ף���ͼ����Ϊһ��Բ���ķ�֮һ�����ѵײ��Ļ���Ϊ8�ߣ��ѵĸ�Ϊ5�ߣ����ѵ�����Ͷѷŵ���Ϊ���٣�����֪1�������ԼΪ1.62�����ߣ�Բ����ԼΪ3��������ѷŵ���Լ�У������� ��ͼ��ʾ�ļ���������һЩ�������ɵģ�����������������ͼ�ǣ�������
��ͼ��ʾ�ļ���������һЩ�������ɵģ�����������������ͼ�ǣ�������


