题目内容
20.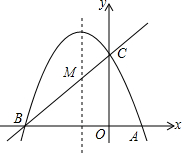 如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,且抛物线经过A(1,0),C(0,3)两点,抛物线与x轴的另一交点为B.
如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,且抛物线经过A(1,0),C(0,3)两点,抛物线与x轴的另一交点为B.(1)若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;
(2)设点P为抛物线的对称轴x=-1上的一个动点,求使△BPC为直角三角形的点P的坐标.
分析 (1)首先由题意根据抛物线的对称性求得点B的坐标,然后利用交点式,求得抛物线的解析式;再利用待定系数法求得直线的解析式;
(2)首先利用勾股定理求得BC,PB,PC的长,然后分别从点B为直角顶点、点C为直角顶点、点P为直角顶点去分析求解即可求得答案.
解答 解:(1)∵抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-1,且抛物线经过A(1,0),抛物线与x轴的另一交点为B,
∴B的坐标为:(-3,0),
设抛物线的解析式为:y=a(x-1)(x+3),
把C(0,3)代入,-3a=3,
解得:a=-1,
∴抛物线的解析式为:y=-(x-1)(x+3)=-x2-2x+3;
把B(-3,0),C(0,3)代入y=mx+n得:
$\left\{\begin{array}{l}{-3m+n=0}\\{n=3}\end{array}\right.$,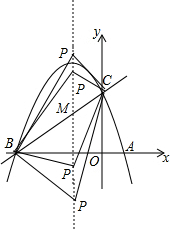
解得:$\left\{\begin{array}{l}{m=1}\\{n=3}\end{array}\right.$,
∴直线y=mx+n的解析式为:y=x+3;
(2)设P(-1,t),
又∵B(-3,0),C(0,3),
∴BC2=18,PB2=(-1+3)2+t2=4+t2,PC2=(-1)2+(t-3)2=t2-6t+10,
①若点B为直角顶点,则BC2+PB2=PC2,
即:18+4+t2=t2-6t+10,解之得:t=-2;
②若点C为直角顶点,则BC2+PC2=PB2,
即:18+t2-6t+10=4+t2,解之得:t=4,
③若点P为直角顶点,则PB2+PC2=BC2,
即:4+t2+t2-6t+10=18,
解之得:t1=$\frac{3+\sqrt{17}}{2}$,t2=$\frac{3-\sqrt{17}}{2}$;
综上所述P的坐标为(-1,-2)或(-1,4)或(-1,$\frac{3+\sqrt{17}}{2}$) 或(-1,$\frac{3-\sqrt{17}}{2}$).
点评 本题综合考查了二次函数的图象与性质、待定系数法求函数(二次函数和一次函数)的解析式以及直角三角形的性质.注意掌握分类讨论思想的应用是解此题的关键.

| A. | 1.0(精确到十分位) | B. | 1.051(精确到千分位) | ||
| C. | 1.10(精确到0.01) | D. | 1.050(精确到0.001) |
 直线l1:y=k1x与直线l2:y=k2x+b在同一平面直角坐标系中的图形如图所示,则关于x的不等式k2x+b≥k1x的解集为( )
直线l1:y=k1x与直线l2:y=k2x+b在同一平面直角坐标系中的图形如图所示,则关于x的不等式k2x+b≥k1x的解集为( )| A. | x≥2 | B. | x≤2 | C. | x≥1 | D. | x≤1 |
| A. | 2(x2-y2) | B. | 2(x+y)(x-y) | C. | 2(x+y)2 | D. | 2(x-y)2 |
| A. | m<-6 | B. | m<-6且m≠-4 | C. | m>-6 | D. | m>-6且m≠-4 |
 如图,AB、CD都是⊙O的弦,且AB⊥CD,若∠CDB=57°,则∠ACD的度数为( )
如图,AB、CD都是⊙O的弦,且AB⊥CD,若∠CDB=57°,则∠ACD的度数为( )| A. | 33° | B. | 34° | C. | 43° | D. | 57° |
| A. | 全等三角形的对应角相等 | |
| B. | 如果在一个三角形中,两边相等,那么它们所对的角也相等 | |
| C. | 同位角相等,两直线平行 | |
| D. | 角平分线上的点到这个角的两边的距离相等 |