题目内容
7.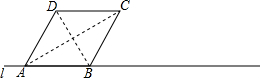 如图,菱形ABCD放置在直线l上(AB与直线l重合),AB=4,∠DAB=60°,将菱形ABCD沿直线l向右无滑动地在直线l上滚动,从点A离开出发点到点A第一次落在直线l上为止,点A运动经过的路径的长度为( )
如图,菱形ABCD放置在直线l上(AB与直线l重合),AB=4,∠DAB=60°,将菱形ABCD沿直线l向右无滑动地在直线l上滚动,从点A离开出发点到点A第一次落在直线l上为止,点A运动经过的路径的长度为( )| A. | $\frac{8π}{3}$$+\frac{8\sqrt{3}π}{3}$ | B. | $\frac{16π}{3}$ | C. | $\frac{4π}{3}$+$\frac{4\sqrt{3}π}{3}$ | D. | $\frac{16\sqrt{3}π}{3}$ |
分析 画出图象即可知道从点A离开出发点到点A第一次落在直线l上为止,点A运动经过的路径的长度为图中弧线长,由此即可解决问题.
解答 解:如图,从点A离开出发点到点A第一次落在直线l上为止,点A运动经过的路径的长度为图中弧线长.
由题意可知$\widehat{AD}$=$\widehat{{A}_{2}{A}_{3}}$,∠DOA2=120°,DO=4$\sqrt{3}$
所以点A运动经过的路径的长度=2×$\frac{60π•4}{180}$+$\frac{120π•4\sqrt{3}}{180}$=$\frac{8}{3}$π+$\frac{8\sqrt{3}}{3}$π,
故选A.
点评 本题考查菱形的性质、弧长公式等知识,解题的关键是正确画出图象,探究点A的运动轨迹,记住弧长公式=$\frac{nπR}{180}$,属于中考常考题型.

练习册系列答案
相关题目
12.已知关于x的方程$\frac{2x+m}{x-2}=3$的解是正数,则m的取值范围为( )
| A. | m<-6 | B. | m<-6且m≠-4 | C. | m>-6 | D. | m>-6且m≠-4 |
19.在下列性质中,矩形具有而菱形不一定有的是( )
| A. | 四个角是直角 | B. | 四条边相等 | C. | 对角线互相垂直 | D. | 对角线互相平分 |
17. 如图,已知AB是⊙O的直径,AC是弦,CD切⊙O于点C,交AB的延长线于点D,∠ACD=120°,BD=10cm,则⊙O的半径为( )
如图,已知AB是⊙O的直径,AC是弦,CD切⊙O于点C,交AB的延长线于点D,∠ACD=120°,BD=10cm,则⊙O的半径为( )
 如图,已知AB是⊙O的直径,AC是弦,CD切⊙O于点C,交AB的延长线于点D,∠ACD=120°,BD=10cm,则⊙O的半径为( )
如图,已知AB是⊙O的直径,AC是弦,CD切⊙O于点C,交AB的延长线于点D,∠ACD=120°,BD=10cm,则⊙O的半径为( )| A. | 5cm | B. | 8cm | C. | 10cm | D. | 12cm |
 如图,桌面上有一个球和一个圆柱形茶叶罐靠在一起,则主视图正确的是( )
如图,桌面上有一个球和一个圆柱形茶叶罐靠在一起,则主视图正确的是( )



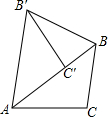 如图,把△ABC绕点A逆时针旋转42°,得到△AB′C′,点C′恰好落在边AB上,连接BB′,则∠B′BC′的大小为69°.
如图,把△ABC绕点A逆时针旋转42°,得到△AB′C′,点C′恰好落在边AB上,连接BB′,则∠B′BC′的大小为69°.