题目内容
⊙O1和⊙O2的半径分别为3和2,O1O2=4,A,B为两圆的交点,则AB= .
考点:相交两圆的性质
专题:
分析:本题可将原图转化成直角三角形求解,连接AO1、AO2形成两个直角三角形,再根据勾股定理即可求出AB的值.
解答: 解:连接O1A,O2A,设O1C=x,则O2C=4-x,
解:连接O1A,O2A,设O1C=x,则O2C=4-x,
∵AC=
=
,
∴
=
,
解得:x=
,O2C=4-x=
;
∴AC=
,
∴AC=
,
∴AB=
.
故答案为:
.
 解:连接O1A,O2A,设O1C=x,则O2C=4-x,
解:连接O1A,O2A,设O1C=x,则O2C=4-x,∵AC=
| O1A2-CO12 |
| O2A2-O2C2 |
∴
| 32-x2 |
| 22-(4-x)2 |
解得:x=
| 21 |
| 8 |
| 11 |
| 8 |
∴AC=
22-(
|
∴AC=
3
| ||
| 8 |
∴AB=
3
| ||
| 4 |
故答案为:
3
| ||
| 4 |
点评:此题考查了相交两圆的性质和直角三角形的性质,解此类题目要注意将圆的问题转化成三角形的问题再进行计算.

练习册系列答案
相关题目
从装有7种颜色每色77个球的袋中摸球出来,摸时没法判断颜色,要确保摸出的球装满7盒,每盒7个球,盒中的球同色,则至少需要摸出( )个球.
| A、85 | B、84 | C、71 | D、50 |
 如图.AB是⊙0的直径,C是⊙0上的一点,AB=10,tanA=
如图.AB是⊙0的直径,C是⊙0上的一点,AB=10,tanA=| 3 |
| 4 |
| A、3 | B、4 | C、5 | D、6 |
计算(tan30°)2+(sin45°)2的值是( )
A、
| ||
B、
| ||
C、
| ||
| D、1 |
 如图,两个邻接的正方形的面积分别为4和196,那么,这两个正方形内切圆圆心距是( )
如图,两个邻接的正方形的面积分别为4和196,那么,这两个正方形内切圆圆心距是( )| A、10 | ||
B、8
| ||
C、10
| ||
| D、8 |
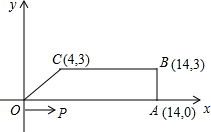 如图,梯形OABC中,O为直角坐标系的原点,A、B、C的坐标分别为A(14,0)、B(14,3)、C(4,3),点P、Q为两动点,同时从原点出发,分别作匀速运动,其中P点沿OA向终点A运动,速度为每秒1个单位;点Q沿OC、CB向终点B运动,速度为每秒2个单位.且当这两点中有一点到达自己的终点时,另一点也停止运动.设运动的时间为t秒.
如图,梯形OABC中,O为直角坐标系的原点,A、B、C的坐标分别为A(14,0)、B(14,3)、C(4,3),点P、Q为两动点,同时从原点出发,分别作匀速运动,其中P点沿OA向终点A运动,速度为每秒1个单位;点Q沿OC、CB向终点B运动,速度为每秒2个单位.且当这两点中有一点到达自己的终点时,另一点也停止运动.设运动的时间为t秒. 把正奇数依次排列成5列,如右图,则2001排在从左数第
把正奇数依次排列成5列,如右图,则2001排在从左数第