题目内容
从装有7种颜色每色77个球的袋中摸球出来,摸时没法判断颜色,要确保摸出的球装满7盒,每盒7个球,盒中的球同色,则至少需要摸出( )个球.
| A、85 | B、84 | C、71 | D、50 |
考点:排列与组合问题
专题:方案型
分析:由题意可知,只要够七个就能装一盒,最多13个同色的能装一盒,前6种取完后,第七种只要够7个就一定能完成任务.
解答:解:前六种需要13×6=78个,第七种摸完7个不论是何种颜色都可以完成.
78+7=85.
故选A.
78+7=85.
故选A.
点评:本题主要考查了排列组合问题,找出只能装一盒的最大数是解答本题的关键.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
假设计算式“a#a+b”表示经过计算后a的值变为a的原值和b的原值的和:又“b#b•c”表示经过计算后b的值变为b的原值和c的原值的乘积.假设计算开始时a=0,b=1,c=1.对a,b,c同时进行以下计算:(1)a#a+b;(2)b#b•c;(3)c#a+b+c(即c的值变为所得到的a,b的值和c的原值的和).连续进行上述运算共三次,则计算结束时a,b,c三个数之和是( )
| A、1位数 | B、2位数 |
| C、3位数 | D、4位数 |
矩形DEFG内接于等边三角形ABC,若EG⊥AC,则四边形ABEG与三角形CEG的面积比值为( )
A、
| ||
| B、2 | ||
C、
| ||
D、
|
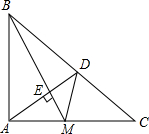 如图,设点M是等腰Rt△ABC的直角边AC的中点,AD⊥BM于E,AD交BC于D.求证:∠AMB=∠CMD(请用两种不同的方法证明)
如图,设点M是等腰Rt△ABC的直角边AC的中点,AD⊥BM于E,AD交BC于D.求证:∠AMB=∠CMD(请用两种不同的方法证明)