题目内容
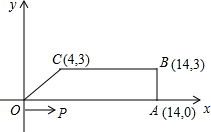 如图,梯形OABC中,O为直角坐标系的原点,A、B、C的坐标分别为A(14,0)、B(14,3)、C(4,3),点P、Q为两动点,同时从原点出发,分别作匀速运动,其中P点沿OA向终点A运动,速度为每秒1个单位;点Q沿OC、CB向终点B运动,速度为每秒2个单位.且当这两点中有一点到达自己的终点时,另一点也停止运动.设运动的时间为t秒.
如图,梯形OABC中,O为直角坐标系的原点,A、B、C的坐标分别为A(14,0)、B(14,3)、C(4,3),点P、Q为两动点,同时从原点出发,分别作匀速运动,其中P点沿OA向终点A运动,速度为每秒1个单位;点Q沿OC、CB向终点B运动,速度为每秒2个单位.且当这两点中有一点到达自己的终点时,另一点也停止运动.设运动的时间为t秒.(1)写出点Q分别在OC和CB上时的坐标(用含t 的代数式表示).
(2)是否存在t的值,使得OPQC为等腰梯形?若存在,求出相应的t 值和P、Q两点的坐标;若不存在,请说明理由.
(3)是否存在t的值,使得PQ把梯形OABC的面积分成相等的两部分?若存在,求出相应的t值和P、Q的坐标;若不存在,请说明理由.
考点:直角梯形,点的坐标,三角形的面积,等腰梯形的判定
专题:动点型
分析:(1)过点C作CD⊥x轴于点D,根据勾股定理求出OC的长,然后利用相似三角形对应边成比例列式即可求出当点Q在OC上时的坐标;当点Q在CB上时求出CQ的长度,然后根据纵坐标不变写出坐标即可;
(2)先求出时间t的取值范围,再过Q作QE⊥x轴于点E,分别表示出CQ与DE的长度,根据等腰梯形的性质CQ=DE,然后代入进行计算求出t的值,若符合题意则存在,否则不存在;
(3)假设存在,然后根据梯形OABC的面积与梯形OPQC的面积列出算式,解方程得到t的值,如果在范围内,则存在,否则不存在.
(2)先求出时间t的取值范围,再过Q作QE⊥x轴于点E,分别表示出CQ与DE的长度,根据等腰梯形的性质CQ=DE,然后代入进行计算求出t的值,若符合题意则存在,否则不存在;
(3)假设存在,然后根据梯形OABC的面积与梯形OPQC的面积列出算式,解方程得到t的值,如果在范围内,则存在,否则不存在.
解答:解:(1) 过点C作CD⊥x轴于点D,
过点C作CD⊥x轴于点D,
∵C(4,3),
∴OD=4,CD=3,
OC=
=
=5,
①点Q在OC上时,设Q点坐标为(x,y),
则
=
=
,
接到的x=
t,y=
t,
∴点Q的坐标是(
t,
t);
②点Q在CB上时,点Q的横坐标是2t-5+4=2t-1,
纵坐标是3,
∴点Q的坐标是(2t-1,3);
(2)点P到达终点A的时间为:14÷1=14秒,
点Q到达终点B的时间为:(14-4+5)÷2=7.5秒,
∵有一点到达自己的终点时,另一点也停止运动,
∴运动时间t的取值范围是0≤t≤7.5,
设存在t的值,使得OPQC为等腰梯形,
过点Q作QE⊥x轴于点E,则DE=t-4×2=t-8,
CQ=2t-OC=2t-5,
∴t-8=2t-5,
解得t=-3,不符合题意,
∴不存在t的值,使得OPQC为等腰梯形;
(3)梯形OABC的面积=
(14-4+14)×3=36,
∵CQ=2t-5,OP=t,
∴梯形OPQC的面积=
(2t-5+t)×3=
,
∵PQ把梯形OABC的面积分成相等的两部分,
∴
=
×36,
解得t=
秒,
∵0<
<7.5,
∴存在t=
,使得PQ把梯形OABC的面积分成相等的两部分,
此时,点P的坐标是(
,0),
点Q的横坐标是2×
-1=
,纵坐标是3,
∴点Q的坐标是(
,3).
 过点C作CD⊥x轴于点D,
过点C作CD⊥x轴于点D,∵C(4,3),
∴OD=4,CD=3,
OC=
| OD2+CD2 |
| 42+32 |
①点Q在OC上时,设Q点坐标为(x,y),
则
| x |
| 4 |
| y |
| 3 |
| 2t |
| 5 |
接到的x=
| 8 |
| 5 |
| 6 |
| 5 |
∴点Q的坐标是(
| 8 |
| 5 |
| 6 |
| 5 |
②点Q在CB上时,点Q的横坐标是2t-5+4=2t-1,
纵坐标是3,
∴点Q的坐标是(2t-1,3);
(2)点P到达终点A的时间为:14÷1=14秒,
点Q到达终点B的时间为:(14-4+5)÷2=7.5秒,
∵有一点到达自己的终点时,另一点也停止运动,
∴运动时间t的取值范围是0≤t≤7.5,
设存在t的值,使得OPQC为等腰梯形,
过点Q作QE⊥x轴于点E,则DE=t-4×2=t-8,
CQ=2t-OC=2t-5,
∴t-8=2t-5,
解得t=-3,不符合题意,
∴不存在t的值,使得OPQC为等腰梯形;
(3)梯形OABC的面积=
| 1 |
| 2 |
∵CQ=2t-5,OP=t,
∴梯形OPQC的面积=
| 1 |
| 2 |
| 9t-15 |
| 2 |
∵PQ把梯形OABC的面积分成相等的两部分,
∴
| 9t-15 |
| 2 |
| 1 |
| 2 |
解得t=
| 17 |
| 3 |
∵0<
| 17 |
| 3 |
∴存在t=
| 17 |
| 3 |
此时,点P的坐标是(
| 17 |
| 3 |
点Q的横坐标是2×
| 17 |
| 3 |
| 31 |
| 3 |
∴点Q的坐标是(
| 31 |
| 3 |
点评:本题综合考查了直角梯形,等腰梯形的性质,以及点的坐标,理清点P与点Q的运动过程以及相关的线段的长度的表示是解题的关键.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
 如图中,以A,B,C,D,E,F,G,H这些点为端点的线段共有
如图中,以A,B,C,D,E,F,G,H这些点为端点的线段共有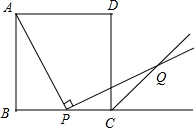 (1)如图,P是正方形ABCD的BC边上的中点,AP⊥PQ,且PQ交∠DCB的外角平分线于Q.求证:AP=PQ
(1)如图,P是正方形ABCD的BC边上的中点,AP⊥PQ,且PQ交∠DCB的外角平分线于Q.求证:AP=PQ 如图中有四个面积相同的圆,每个圆的面积都记为S,∠ABC的两边分别经过圆心O1、O2、O3和O4,四个圆盖的面积为5(S-1),∠ABC内部被圆盖住的面积为8,阴影部分的面积为S1、S2、S3满足关系式:
如图中有四个面积相同的圆,每个圆的面积都记为S,∠ABC的两边分别经过圆心O1、O2、O3和O4,四个圆盖的面积为5(S-1),∠ABC内部被圆盖住的面积为8,阴影部分的面积为S1、S2、S3满足关系式: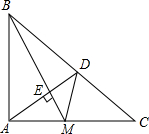 如图,设点M是等腰Rt△ABC的直角边AC的中点,AD⊥BM于E,AD交BC于D.求证:∠AMB=∠CMD(请用两种不同的方法证明)
如图,设点M是等腰Rt△ABC的直角边AC的中点,AD⊥BM于E,AD交BC于D.求证:∠AMB=∠CMD(请用两种不同的方法证明)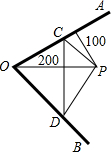 如图,两条河交汇于O点,夹75°角,旅行家住在P点,离O点200m,离河岸AO100cm.他希望到AO上任一点处欣赏风光,再折到河岸BO上任一点D处眺望景物,然后回到住地,则旅行家最少要走
如图,两条河交汇于O点,夹75°角,旅行家住在P点,离O点200m,离河岸AO100cm.他希望到AO上任一点处欣赏风光,再折到河岸BO上任一点D处眺望景物,然后回到住地,则旅行家最少要走