题目内容
已知bc-a2=5,ca-b2=-1,ab-c2=-7,则6a+7b+8c= .
考点:对称式和轮换对称式
专题:
分析:令bc-a2=5…①,ca-b2=-1…②,ac-c2=-7…③,用①式减②式得 bc-a2-ca+b2=c(b-a)+(b+a)(b-a)=(a+b+c)(b-a)=6,②式减③式得 ca-b2-ab+c2=a(c-b)+(c+b)(c-b)=(a+b+c)(c-b)=6,于是求出b和a、c之间的关系,进一步讨论求出a、b和c的值,6a+7b+8c的值即可求出.
解答:解:令bc-a2=5…①,ca-b2=-1…②,ac-c2=-7…③,
①式减②式得 bc-a2-ca+b2=c(b-a)+(b+a)(b-a)=(a+b+c)(b-a)=6,
②式减③式得 ca-b2-ab+c2=a(c-b)+(c+b)(c-b)=(a+b+c)(c-b)=6,
所以b-a=c-b,即b=
,代入②得 ca-
=-1,
4ac-(a+c)2=-4,(a-c)2=4,a-c=2或a-c=4,
当a-c=2时,a=c+2,b=
=c+1,代入③式得(c+2)(c+1)-c2=-7,3c+2=-7,c=-3,
所以a=-1,b=-2,此时6a+7b+8c=6×(-1)+7×(-2)+8×(-3)=-44,
当a-c=-2时,a=c-2,b=
=c-1,代入③式得(c-2)(c-1)-c2=-7-3c+2=-7,c=3,
所以a=1,b=2 此时6a+7b+8c=6×1+7×2+8×3=44,
所以6a+7b+8c=-44或6a+7b+8c=44,
故答案为44或-44.
①式减②式得 bc-a2-ca+b2=c(b-a)+(b+a)(b-a)=(a+b+c)(b-a)=6,
②式减③式得 ca-b2-ab+c2=a(c-b)+(c+b)(c-b)=(a+b+c)(c-b)=6,
所以b-a=c-b,即b=
| a+c |
| 2 |
| (a+c)2 |
| 4 |
4ac-(a+c)2=-4,(a-c)2=4,a-c=2或a-c=4,
当a-c=2时,a=c+2,b=
| a+c |
| 2 |
所以a=-1,b=-2,此时6a+7b+8c=6×(-1)+7×(-2)+8×(-3)=-44,
当a-c=-2时,a=c-2,b=
| a+c |
| 2 |
所以a=1,b=2 此时6a+7b+8c=6×1+7×2+8×3=44,
所以6a+7b+8c=-44或6a+7b+8c=44,
故答案为44或-44.
点评:本题主要考查对称式和轮换对称式的知识点,解答本题的关键是求出b=
,此题难度不大.
| a+c |
| 2 |

练习册系列答案
相关题目
假设计算式“a#a+b”表示经过计算后a的值变为a的原值和b的原值的和:又“b#b•c”表示经过计算后b的值变为b的原值和c的原值的乘积.假设计算开始时a=0,b=1,c=1.对a,b,c同时进行以下计算:(1)a#a+b;(2)b#b•c;(3)c#a+b+c(即c的值变为所得到的a,b的值和c的原值的和).连续进行上述运算共三次,则计算结束时a,b,c三个数之和是( )
| A、1位数 | B、2位数 |
| C、3位数 | D、4位数 |
下列哪个不是方程
+
=0的解( )
| x-y | 9 |
| 3 | x+y |
| A、(-3,-6) |
| B、(-12.5,-14.5) |
| C、(-364,-365) |
| D、(-0.5,-0.5) |
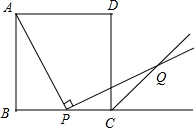 (1)如图,P是正方形ABCD的BC边上的中点,AP⊥PQ,且PQ交∠DCB的外角平分线于Q.求证:AP=PQ
(1)如图,P是正方形ABCD的BC边上的中点,AP⊥PQ,且PQ交∠DCB的外角平分线于Q.求证:AP=PQ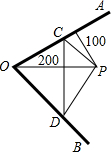 如图,两条河交汇于O点,夹75°角,旅行家住在P点,离O点200m,离河岸AO100cm.他希望到AO上任一点处欣赏风光,再折到河岸BO上任一点D处眺望景物,然后回到住地,则旅行家最少要走
如图,两条河交汇于O点,夹75°角,旅行家住在P点,离O点200m,离河岸AO100cm.他希望到AO上任一点处欣赏风光,再折到河岸BO上任一点D处眺望景物,然后回到住地,则旅行家最少要走