题目内容
已知不等式ax2-2x-a+1<0,当-2≤a≤2时恒成立,求x的取值范围.
考点:抛物线与x轴的交点
专题:计算题
分析:令y=ax2-2x-a+1=(x2-1)a+(-2x+1),由于当x=1时,y<0;当x=-1时,y>0,所以x=1满足条件;若x≠±1时,y是关于a的一次函数,根据一次函数的性质得到-2(x2-1)+(-2x+1)<0且2(x2-1)+(-2x+1)<0,整理得2x2+2x-3>0且2x2-2x-1<0,然后根据抛物线与x轴的交点问题解两个不等式,再写出它们的公共部分,于是可确定满足条件的x的取值范围.
解答:解:设y=ax2-2x-a+1=(x2-1)a+(-2x+1),
当x=1时,y<0;当x=-1时,y>0,
若x≠±1时,y是关于a的一次函数,
因为-2≤a≤2时,y<0,
所以-2(x2-1)+(-2x+1)<0且2(x2-1)+(-2x+1)<0,
对于-2(x2-1)+(-2x+1)<0整理得2x2+2x-3>0,解方程2x2+2x-3=0得x1=
,x2=
,所以2x2+2x-3>0的解集为x>
或x<
;
对于2(x2-1)+(-2x+1)<0整理得2x2-2x-1<0,解方程2x2-2x-1=0得x1=
,x2=
,所以2x2-2x-1<0的解集为
<x<
,
所以
<x<
或x=-1.
当x=1时,y<0;当x=-1时,y>0,
若x≠±1时,y是关于a的一次函数,
因为-2≤a≤2时,y<0,
所以-2(x2-1)+(-2x+1)<0且2(x2-1)+(-2x+1)<0,
对于-2(x2-1)+(-2x+1)<0整理得2x2+2x-3>0,解方程2x2+2x-3=0得x1=
-1+
| ||
| 2 |
-1-
| ||
| 2 |
-1+
| ||
| 2 |
-1-
| ||
| 2 |
对于2(x2-1)+(-2x+1)<0整理得2x2-2x-1<0,解方程2x2-2x-1=0得x1=
1+
| ||
| 2 |
1-
| ||
| 2 |
1-
| ||
| 2 |
1+
| ||
| 2 |
所以
-1+
| ||
| 2 |
1+
| ||
| 2 |
点评:本题考查了抛物线与x轴的交点:求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标,令y=0,即ax2+bx+c=0,解关于x的一元二次方程即可求得交点横坐标.对于二次函数y=ax2+bx+c(a,b,c是常数,a≠0),△=b2-4ac决定抛物线与x轴的交点个数,△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.也考查了二次函数的性质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,在?ABCD中,点E,F分别为边BC,AD的中点.
如图,在?ABCD中,点E,F分别为边BC,AD的中点.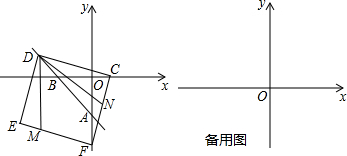
 有一把折扇,已知折扇的骨柄长为30cm,折扇扇面的宽度是骨柄长的一半,折扇张开的角度为120°,若要改用一把圆扇,则圆扇的直径应是多少才能得到与折扇面积一样的风量.
有一把折扇,已知折扇的骨柄长为30cm,折扇扇面的宽度是骨柄长的一半,折扇张开的角度为120°,若要改用一把圆扇,则圆扇的直径应是多少才能得到与折扇面积一样的风量.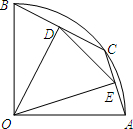 如图,在半径为2的扇形OAB中,∠AOB=90°,点C是
如图,在半径为2的扇形OAB中,∠AOB=90°,点C是
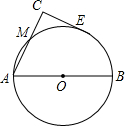 如图,AB为⊙O的直径,CE与⊙O相切于E,AC⊥CE于C,AC交⊙O于M,若AM=2CM=2,求CE的长.
如图,AB为⊙O的直径,CE与⊙O相切于E,AC⊥CE于C,AC交⊙O于M,若AM=2CM=2,求CE的长.