题目内容
如图,直线l与y轴、x轴分别交于点A(0,-2)和点B(-
,0).
(1)求直线l的解析式;
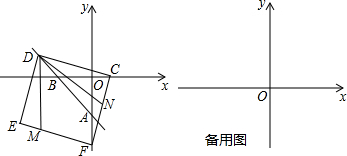
(2)点D是直线l上的一个动点,C点的坐标是(1,0),以CD为边在一侧作正方形CDEF(如图所示),当正方形的一个顶点恰好落在y轴上时(D点除外),求出对应的D点的坐标;
(3)若点M、点N分别为边EF和FC上的两个点,并且∠MDN=45°,问:在点D运动的过程中,△FMN的周长是否存在最小值?若存在,求出周长的最小值;若不存在,请说明理由.
| 3 |
| 2 |

(1)求直线l的解析式;
(2)点D是直线l上的一个动点,C点的坐标是(1,0),以CD为边在一侧作正方形CDEF(如图所示),当正方形的一个顶点恰好落在y轴上时(D点除外),求出对应的D点的坐标;
(3)若点M、点N分别为边EF和FC上的两个点,并且∠MDN=45°,问:在点D运动的过程中,△FMN的周长是否存在最小值?若存在,求出周长的最小值;若不存在,请说明理由.
考点:一次函数综合题
专题:常规题型
分析:(1)将A,B两点代入直线解析式y=kx+b,即可求得k,b的值即可解题;
(2)正方形顶点F落于y轴上,且C点横坐标为1,可得D点纵坐标为1,即可求得D点坐标;
(3)易证△FMN的周长为正方形CDEF边长的2倍,即可求得△FMN的周长存在最小值时D点坐标.
(2)正方形顶点F落于y轴上,且C点横坐标为1,可得D点纵坐标为1,即可求得D点坐标;
(3)易证△FMN的周长为正方形CDEF边长的2倍,即可求得△FMN的周长存在最小值时D点坐标.
解答:解:(1)设直线l解析式为y=kx+b,
∵A,B两点在直线l上,
∴b=-2,k=-
,
∴直线l解析式为y=-
x-2;
(2)正方形顶点F落于y轴上,且C点横坐标为1,
∴D点纵坐标为1,
将y=1,代入y=-
-2中,得x=-
.
∴D点坐标为(-
,1);
(3)将△DCN向左旋转90°得到△DEQ,

∵CD=DE,∴Q,E,F三点一线,
∵DMN=45°,∴∠QDM=∠EDM+∠CDN=45°,
在△DMQ和△DMN中,
,
∴△DMQ≌△DMN(SAS),
∴MN=QM=EM+CN,
∴△FMN周长=FM+FN+MN=2CD,
∴在点D运动的过程中,△FMN的周长存在最小值.
即让CD最短即可,C点到直线l最短距离为垂线段长度,即CD⊥l即可,
∴直线CD的斜率
,
设直线CD解析式为y=
x+b,
∵直线CD经过C点,代入C点坐标得b=-
,
直线CD解析式为y=
x-
,
直线CD与l的交点为(-
,-
),
故点D坐标为(-
,-
)时,△FMN周长有最小值为4.
∵A,B两点在直线l上,
∴b=-2,k=-
| 4 |
| 3 |
∴直线l解析式为y=-
| 4 |
| 3 |
(2)正方形顶点F落于y轴上,且C点横坐标为1,
∴D点纵坐标为1,
将y=1,代入y=-
| 4 |
| 3 |
| 9 |
| 4 |
∴D点坐标为(-
| 9 |
| 4 |
(3)将△DCN向左旋转90°得到△DEQ,

∵CD=DE,∴Q,E,F三点一线,
∵DMN=45°,∴∠QDM=∠EDM+∠CDN=45°,
在△DMQ和△DMN中,
|
∴△DMQ≌△DMN(SAS),
∴MN=QM=EM+CN,
∴△FMN周长=FM+FN+MN=2CD,
∴在点D运动的过程中,△FMN的周长存在最小值.
即让CD最短即可,C点到直线l最短距离为垂线段长度,即CD⊥l即可,
∴直线CD的斜率
| 3 |
| 4 |
设直线CD解析式为y=
| 3 |
| 4 |
∵直线CD经过C点,代入C点坐标得b=-
| 3 |
| 4 |
直线CD解析式为y=
| 3 |
| 4 |
| 3 |
| 4 |
直线CD与l的交点为(-
| 3 |
| 5 |
| 6 |
| 5 |
故点D坐标为(-
| 3 |
| 5 |
| 6 |
| 5 |
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,考查了一次函数的交点问题,本题中求证△FMN周长是CD长的2倍是解题的关键.

练习册系列答案
相关题目
-5的相反数的倒数是( )
A、
| ||
| B、-5 | ||
C、-
| ||
| D、5 |