题目内容
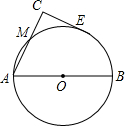 如图,AB为⊙O的直径,CE与⊙O相切于E,AC⊥CE于C,AC交⊙O于M,若AM=2CM=2,求CE的长.
如图,AB为⊙O的直径,CE与⊙O相切于E,AC⊥CE于C,AC交⊙O于M,若AM=2CM=2,求CE的长.考点:切线的性质
专题:计算题
分析:连接OE,作OH⊥AM于H,如图,根据切线的性质,由CE与⊙O相切于E得OE⊥CE,再利用垂径定理,由OH⊥AM得AH=MH=
AM=1,则CH=HM+CM=2,再证明四边形CHOE为矩形,得到OE=CH=2,OH=CE,然后在Rt△OAH中利用勾股定理计算出OH,从而得到CE.
| 1 |
| 2 |
解答:解: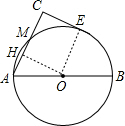 连接OE,作OH⊥AM于H,如图,
连接OE,作OH⊥AM于H,如图,
∵CE与⊙O相切于E,
∴OE⊥CE,
∵OH⊥AM,
∴AH=MH=
AM=
×2=1,
∴CH=HM+CM=1+1=2,
∵AC⊥CE,
∴四边形CHOE为矩形,
∴OE=CH=2,OH=CE,
∴OA=2,
在Rt△OAH中,∵OA=2,AH=1,
∴OH=
=
,
∴CE=
.
 连接OE,作OH⊥AM于H,如图,
连接OE,作OH⊥AM于H,如图,∵CE与⊙O相切于E,
∴OE⊥CE,
∵OH⊥AM,
∴AH=MH=
| 1 |
| 2 |
| 1 |
| 2 |
∴CH=HM+CM=1+1=2,
∵AC⊥CE,
∴四边形CHOE为矩形,
∴OE=CH=2,OH=CE,
∴OA=2,
在Rt△OAH中,∵OA=2,AH=1,
∴OH=
| OA2-AH2 |
| 3 |
∴CE=
| 3 |
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.也考查了垂径定理.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
-5的相反数的倒数是( )
A、
| ||
| B、-5 | ||
C、-
| ||
| D、5 |
已知扇形的半径为3,它的面积等于一个半径为1的圆的面积,则扇形的圆心角为( )
| A、60° | B、40° |
| C、120° | D、80° |
用一个平面去截一个几何体,得到的截面是三角形,这个几何体可能是( )
| A、圆锥 | B、圆柱 |
| C、球体 | D、以上都有可能 |