题目内容
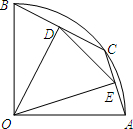 如图,在半径为2的扇形OAB中,∠AOB=90°,点C是
如图,在半径为2的扇形OAB中,∠AOB=90°,点C是 |
| AB |
(1)当BC=2时,求线段OD的长和∠BOD的度数;
(2)在△DOE中,是否存在长度保持不变的边?如果存在,请指出并求其长度;如果不存在,请说明理由.
(3)在△DOE中,是否存在度数保持不变的角?如果存在,请指出并求其度数;如果不存在,请说明理由.
考点:垂径定理,三角形中位线定理
专题:
分析:(1)根据垂径定理及勾股定理即可解决问题;
(2)利用三角形的中位线定理即可解决问题;
(3)利用等腰三角形的性质即可解决问题.
(2)利用三角形的中位线定理即可解决问题;
(3)利用等腰三角形的性质即可解决问题.
解答: 解:(1)如图,
解:(1)如图,
∵OD⊥BC,
∴BD=CD=
BC=1,
∴BD=
OB,
∴∠BOD=30°;
由勾股定理得:
OD2=22-12=3,
∴OD=
;
即线段OD的长和∠BOD的度数分别为
、30°.
(2)存在,DE=
;
如图,连接AB;
∵∠AOB=90°,OA=OB=2,
∴AB2=OB2+OA2=8,
∴AB=2
;
∵OD⊥BC,OE⊥AC,
∴BD=CD,AE=EC,
∴DE是△ABC的中位线,
DE=
×2
=
.
(3)存在,∠DOE=45°;
∵OD⊥BC,OE⊥AC,且OA=OB=OC,
∴∠BOD=∠COD,∠AOE=∠COE,
∴∠DOE=
∠AOB=45°,
即∠DOE=45°.
 解:(1)如图,
解:(1)如图,∵OD⊥BC,
∴BD=CD=
| 1 |
| 2 |
∴BD=
| 1 |
| 2 |
∴∠BOD=30°;
由勾股定理得:
OD2=22-12=3,
∴OD=
| 3 |
即线段OD的长和∠BOD的度数分别为
| 3 |
(2)存在,DE=
| 2 |
如图,连接AB;
∵∠AOB=90°,OA=OB=2,
∴AB2=OB2+OA2=8,
∴AB=2
| 2 |
∵OD⊥BC,OE⊥AC,
∴BD=CD,AE=EC,
∴DE是△ABC的中位线,
DE=
| 1 |
| 2 |
| 2 |
| 2 |
(3)存在,∠DOE=45°;
∵OD⊥BC,OE⊥AC,且OA=OB=OC,
∴∠BOD=∠COD,∠AOE=∠COE,
∴∠DOE=
| 1 |
| 2 |
即∠DOE=45°.
点评:该命题以圆为载体,在考查垂径定理、三角形中位线定理、勾股定理的同时,还渗透了对动态观念、直觉思维等能力的考查;对分析问题解决问题的能力提出了较高的要求.

练习册系列答案
相关题目
两个有理数相加,若和为负数,则加数中正数的个数( )
| A、有2个 | B、只有1个 |
| C、至少1个 | D、至多1个 |