题目内容
19．
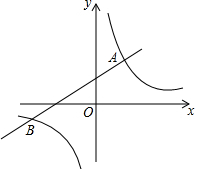如图，在平面直角坐标系xOy中，函数y=kx+b（k≠0）与y=$\frac{m}{x}$（m≠0）的图象相交于点A（2，3），B（-6，-1），则不等式kx+b＞$\frac{m}{x}$的解集为（ ）| A． | x＜-6 | B． | -6＜x＜0或x＞2 | C． | x＞2 | D． | x＜-6或0＜x＜2 |
分析 根据函数的图象和交点坐标即可求得结果．
解答 解：不等式kx+b＞$\frac{m}{x}$的解集为：-6＜x＜0或x＞2，
故选B．
点评 此题考查了反比例函数与一次函数的交点问题，关键是注意掌握数形结合思想的应用．
练习册系列答案
相关题目
9．
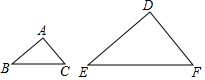如图，已知△ABC∽△DEF，AB：DE=1：2，则下列等式一定成立的是（ ）
如图，已知△ABC∽△DEF，AB：DE=1：2，则下列等式一定成立的是（ ）| A． | $\frac{BC}{DF}$=$\frac{1}{2}$ | B． | $\frac{∠A的度数}{∠D的度数}$=$\frac{1}{2}$ | ||
| C． | $\frac{△ABC的面积}{△DEF的面积}$=$\frac{1}{2}$ | D． | $\frac{△ABC的周长}{△DEF的周长}$=$\frac{1}{2}$ |
10．为了解某市市民“绿色出行”方式的情况，某校数学兴趣小组以问卷调查的形式，随机调查了某市部分出行市民的主要出行方式（参与问卷调查的市民都只从以下五个种类中选择一类），并将调查结果绘制成如下不完整的统计图．
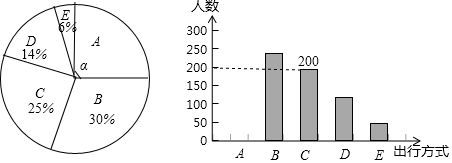
根据以上信息，回答下列问题：
（1）参与本次问卷调查的市民共有800人，其中选择B类的人数有240人；
（2）在扇形统计图中，求A类对应扇形圆心角α的度数，并补全条形统计图；
（3）该市约有12万人出行，若将A，B，C这三类出行方式均视为“绿色出行”方式，请估计该市“绿色出行”方式的人数．
| 种类 | A | B | C | D | E |
| 出行方式 | 共享单车 | 步行 | 公交车 | 的士 | 私家车 |
根据以上信息，回答下列问题：
（1）参与本次问卷调查的市民共有800人，其中选择B类的人数有240人；
（2）在扇形统计图中，求A类对应扇形圆心角α的度数，并补全条形统计图；
（3）该市约有12万人出行，若将A，B，C这三类出行方式均视为“绿色出行”方式，请估计该市“绿色出行”方式的人数．
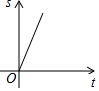
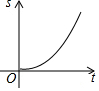
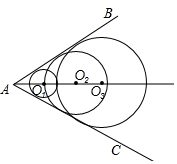如图，∠BAC=60°，点O从A点出发，以2cm/s的速度沿∠BAC的角平分线向右运动，在运动过程中，以O为圆心的圆始终保持与∠BAC的两边相切，设⊙O的面积为S（cm2），则⊙O的面积S与圆心O运动的时间t（s）的函数图象大致为（ ）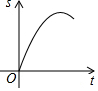
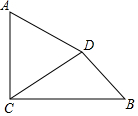14．下列图形中，既是轴对称图形，又是中心对称图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |
如图，已知AC⊥BC，垂足为C，AC=4，BC=3$\sqrt{3}$，将线段AC绕点A按逆时针方向旋转60°，得到线段AD，连接DC，DB．
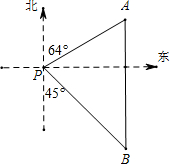如图，一艘海轮位于灯塔P的北偏东64°方向，距离灯塔120海里的A处，它沿正南方向航行一段时间后，到达位于灯塔P的南偏东45°方向上的B处，求BP和BA的长（结果取整数）．