题目内容
9.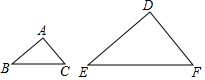 如图,已知△ABC∽△DEF,AB:DE=1:2,则下列等式一定成立的是( )
如图,已知△ABC∽△DEF,AB:DE=1:2,则下列等式一定成立的是( )| A. | $\frac{BC}{DF}$=$\frac{1}{2}$ | B. | $\frac{∠A的度数}{∠D的度数}$=$\frac{1}{2}$ | ||
| C. | $\frac{△ABC的面积}{△DEF的面积}$=$\frac{1}{2}$ | D. | $\frac{△ABC的周长}{△DEF的周长}$=$\frac{1}{2}$ |
分析 根据相似三角形的性质判断即可.
解答 解:∵△ABC∽△DEF,
∴$\frac{BC}{EF}$=$\frac{1}{2}$,A不一定成立;
$\frac{∠A的度数}{∠D的度数}$=1,B不成立;
$\frac{△ABC的面积}{△DEF的面积}$=$\frac{1}{4}$,C不成立;
$\frac{△ABC的周长}{△DEF的周长}$=$\frac{1}{2}$,D成立,
故选:D.
点评 本题考查的是相似三角形的性质,掌握相似三角形的对应角相等,对应边的比相等、相似三角形(多边形)的周长的比等于相似比、相似三角形的面积的比等于相似比的平方是解题的关键.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
20.计算:($\frac{1}{3}$)2•3-1=( )
| A. | $\frac{1}{3}$ | B. | 1 | C. | $\frac{1}{27}$ | D. | -$\frac{1}{27}$ |
4.下列一元二次方程没有实数根的是( )
| A. | x2-2x=0 | B. | x2-1=0 | C. | x2+x+1=0 | D. | x2+2x+1=0 |
1.慈溪,因治南有溪而得名,慈溪的常住人口约为1460000人,1460000用科学记数法表示为( )
| A. | 0.146×107 | B. | 1.46×105 | C. | 14.6×105 | D. | 1.46×106 |
19.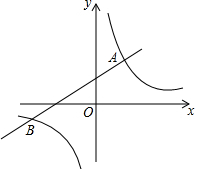 如图,在平面直角坐标系xOy中,函数y=kx+b(k≠0)与y=$\frac{m}{x}$(m≠0)的图象相交于点A(2,3),B(-6,-1),则不等式kx+b>$\frac{m}{x}$的解集为( )
如图,在平面直角坐标系xOy中,函数y=kx+b(k≠0)与y=$\frac{m}{x}$(m≠0)的图象相交于点A(2,3),B(-6,-1),则不等式kx+b>$\frac{m}{x}$的解集为( )
 如图,在平面直角坐标系xOy中,函数y=kx+b(k≠0)与y=$\frac{m}{x}$(m≠0)的图象相交于点A(2,3),B(-6,-1),则不等式kx+b>$\frac{m}{x}$的解集为( )
如图,在平面直角坐标系xOy中,函数y=kx+b(k≠0)与y=$\frac{m}{x}$(m≠0)的图象相交于点A(2,3),B(-6,-1),则不等式kx+b>$\frac{m}{x}$的解集为( )| A. | x<-6 | B. | -6<x<0或x>2 | C. | x>2 | D. | x<-6或0<x<2 |