题目内容
8.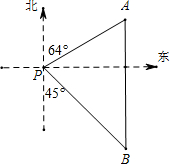 如图,一艘海轮位于灯塔P的北偏东64°方向,距离灯塔120海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,求BP和BA的长(结果取整数).
如图,一艘海轮位于灯塔P的北偏东64°方向,距离灯塔120海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,求BP和BA的长(结果取整数).参考数据:sin64°≈0.90,cos64°≈0.44,tan64°≈2.05,$\sqrt{2}$取1.414.
分析 如图作PC⊥AB于C.分别在Rt△APC,Rt△PCB中求解即可解决问题.
解答 解:如图作PC⊥AB于C.
由题意∠A=64°,∠B=45°,PA=120,
在Rt△APC中,sinA=$\frac{PC}{PA}$,cosA=$\frac{AC}{PC}$,
∴PC=PA•sinA=120•sin64°,
AC=PA•cosA=120•cos64°,
在Rt△PCB中,∵∠B=45°,
∴PC=BC,
∴PB=$\frac{PC}{sin45°}$=$\frac{120×0.90}{\frac{\sqrt{2}}{2}}$≈153.
∴AB=AC+BC=120•cos64°+120•sin64°
≈120×0.90+120×0.44
≈161.
答:BP的长为153海里和BA的长为161海里.
点评 本题考查了解直角三角形的应用--方向角问题,结合航海中的实际问题,将解直角三角形的相关知识有机结合,体现了数学应用于实际生活的思想.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
19.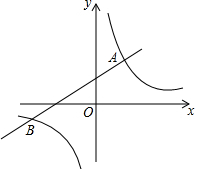 如图,在平面直角坐标系xOy中,函数y=kx+b(k≠0)与y=$\frac{m}{x}$(m≠0)的图象相交于点A(2,3),B(-6,-1),则不等式kx+b>$\frac{m}{x}$的解集为( )
如图,在平面直角坐标系xOy中,函数y=kx+b(k≠0)与y=$\frac{m}{x}$(m≠0)的图象相交于点A(2,3),B(-6,-1),则不等式kx+b>$\frac{m}{x}$的解集为( )
 如图,在平面直角坐标系xOy中,函数y=kx+b(k≠0)与y=$\frac{m}{x}$(m≠0)的图象相交于点A(2,3),B(-6,-1),则不等式kx+b>$\frac{m}{x}$的解集为( )
如图,在平面直角坐标系xOy中,函数y=kx+b(k≠0)与y=$\frac{m}{x}$(m≠0)的图象相交于点A(2,3),B(-6,-1),则不等式kx+b>$\frac{m}{x}$的解集为( )| A. | x<-6 | B. | -6<x<0或x>2 | C. | x>2 | D. | x<-6或0<x<2 |
17.25的算术平方根是( )
| A. | 5 | B. | ±5 | C. | -5 | D. | 25 |
 如图是一个由4个相同的正方体组成的立体图形,它的主视图是( )
如图是一个由4个相同的正方体组成的立体图形,它的主视图是( )



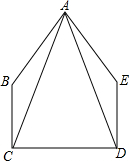 如图,在五边形ABCDE中,∠BCD=∠EDC=90°,BC=ED,AC=AD.
如图,在五边形ABCDE中,∠BCD=∠EDC=90°,BC=ED,AC=AD.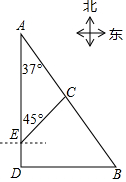 如图,港口B位于港口A的南偏东37°方向,灯塔C恰好在AB的中点处.一艘海轮位于港口A的正南方向,港口B的正西方向的D处,它沿正北方向航行5km到达E处,测得灯塔C在北偏东45°方向上,这时,E处距离港口A有多远?(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
如图,港口B位于港口A的南偏东37°方向,灯塔C恰好在AB的中点处.一艘海轮位于港口A的正南方向,港口B的正西方向的D处,它沿正北方向航行5km到达E处,测得灯塔C在北偏东45°方向上,这时,E处距离港口A有多远?(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)